题目内容
1.已知函数f(x)=ax2+blnx,其中ab≠0,求函数有极值时,a、b满足的条件.分析 由函数f(x)=ax2+blnx,可得f′(x).由题意可得导函数等于0有解.由二次函数函数性质知△>0.
解答 解:∵函敦f(x)=ax2+blnx,其中ab≠0,
∴f(x)的定义域为(0,+∞),
f′(x)=2ax+$\frac{b}{x}$=$\frac{2a{x}^{2}+b}{x}$.
∵函数有极值,
∴f′(x)=0有解,
即2ax2+b=0有解.
∴△>0 即ab<0,两根为x1=$\sqrt{-\frac{b}{2a}}$,x2=-$\sqrt{-\frac{b}{2a}}$(舍去),
f(x)在x1=$\sqrt{-\frac{b}{2a}}$处取得极值.
∴只需ab<0即可.
点评 本题考查函数的导函数与极值之间关系,由有极值,得到导数等于0有解.由导数为0,得到ab的取值范围.

练习册系列答案
相关题目
13.过抛物线C:y2=2px(p>0)的焦点F,且斜率为$\frac{3}{4}$的直线交抛物线C与A,B两点,若$\overrightarrow{AF}$=λ$\overrightarrow{FB}$(0<λ<1),λ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
10.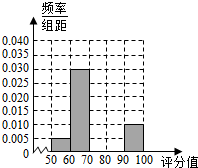 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)将成绩按分层抽样的方法抽取150名同学进行问卷调查,甲同学在本次测试中数学成绩为95分,求他被抽中的概率.
 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
| 成绩分组 | 频数 | 频率 |
| [50,60] | 100 | |
| (60,70] | ||
| (70,80] | 800 | |
| (80,90] | ||
| (90,100] | 200 |
11.设0<a<b,则下列不等式中正确的是( )
| A. | a<b<$\sqrt{ab}$<$\frac{a+b}{2}$ | B. | a<$\sqrt{ab}$<$\frac{a+b}{2}$<b | C. | a<$\sqrt{ab}$<b<$\frac{a+b}{2}$ | D. | $\sqrt{ab}$<a<$\frac{a+b}{2}$<b |