题目内容
18．某高校文学院和理学院的学生组队参加大学生电视辩论赛，文学院推荐了2名男生，3名女生，理学院推荐了4名男生，3名女生，文学院和理学院所推荐的学生一起参加集训，由于集训后学生水平相当，从参加集训的男生中随机抽取3人，女生中随机抽取3人组成代表队．（1）求文学院至少有一名学生入选代表队的概率；
（2）某场比赛前，从代表队的6名学生在随机抽取4名参赛，记X表示参赛的男生人数，求X的分布列与数学期望．
分析 （1）求出文学院至少有一名学生入选代表队的对立事件的概率，然后求解概率即可；
（2）求出X表示参赛的男生人数的可能值，求出概率，得到X的分布列，然后求解数学期望．
解答 解：（1）由题意，参加集训的男、女学生共有6人，参赛学生全从理学院中抽出（等价于文学院中没有学生入选代表队）的概率为：$\frac{{C}_{3}^{3}{C}_{4}^{3}}{{C}_{6}^{3}{C}_{6}^{3}}$=$\frac{1}{100}$，因此文学院至少有一名学生入选代表队的概率为：1-$\frac{1}{100}$=$\frac{99}{100}$；
（Ⅱ）某场比赛前，从代表队的6名队员中随机抽取4人参赛，X表示参赛的男生人数，
则X的可能取值为：1，2，3，
P（X=1）=$\frac{{C}_{3}^{1}{C}_{3}^{3}}{{C}_{6}^{4}}$=$\frac{1}{5}$，P（X=2）=$\frac{{C}_{3}^{2}{C}_{3}^{2}}{{C}_{6}^{4}}$=$\frac{3}{5}$，P（X=3）=$\frac{{C}_{3}^{1}{C}_{3}^{3}}{{C}_{6}^{4}}$=$\frac{1}{5}$．
X的分布列：
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查离散型随机变量的分布列，期望的求法，考查古典概型概率的求法，考查分析问题解决问题的能力．
练习册系列答案
名校课堂系列答案
相关题目
9．已知函数y=2sin（$\frac{x}{2}$-$\frac{π}{4}$）
（1）用“五点法”作出函数图象；
（2）指出它可由函数y=sinx的图象经过哪些变换而得到；
（3）写出函数的单调增区间．
（1）用“五点法”作出函数图象；
（2）指出它可由函数y=sinx的图象经过哪些变换而得到；
（3）写出函数的单调增区间．
6．已知点A（0，2），B（4，0），C（-2，1），若直线CD与直线AB相交，且交点D在线段AB上，直线CD的斜率为k，求$k+\frac{1}{2}+\frac{1}{{k+\frac{1}{2}}}$的取值范围（ ）
| A． | .$（2，\frac{10}{3}）$ | B． | $（-∞，\frac{10}{3}）$ | C． | $[2，\frac{10}{3}]$ | D． | [2，+∞） |
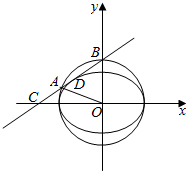已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），点B为圆O：x2+y2=a2与y轴的交点，过点B的直线l（斜率为正）与椭圆相切于点D，并交x轴于点C，O为坐标原点，如图．