题目内容
9.如图,在△ABC中,N、P分别是AC、BN的中点,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AP}$=( )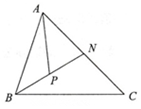
| A. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | B. | -$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | -$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ |
分析 根据向量的加减的几何意义和三角形法则即可求出.
解答 解:$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BN}$,
=-$\overrightarrow{BA}$+$\frac{1}{2}$($\overrightarrow{BC}$-$\overrightarrow{NC}$),
=-$\overrightarrow{BA}$+$\frac{1}{2}$($\overrightarrow{BC}$-$\frac{1}{2}$$\overrightarrow{AC}$),
=-$\overrightarrow{BA}$+$\frac{1}{2}$$\overrightarrow{BC}$-$\frac{1}{4}$($\overrightarrow{AB}$+$\overrightarrow{BC}$),
=-$\frac{3}{4}$$\overrightarrow{BA}$+$\frac{1}{4}$$\overrightarrow{BC}$,
=-$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$,
故选:B
点评 本题考查了向量的加减的几何意义和三角形法则,属于基础题.

练习册系列答案
相关题目
20.某学校需从3名男生和2名女生中选出4人,分派到甲、乙、丙三地参加义工活动,其中甲地需要选派2人且至少有1名女生,乙地和丙地各需要选派1人,则不同的选派方法的种数是( )
| A. | 18 | B. | 24 | C. | 36 | D. | 42 |
4.函数f(x)=sin(πx+θ)(|θ|<$\frac{π}{2}$)的部分图象如图,且f(0)=-$\frac{1}{2}$,则图中m的值为( )
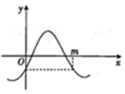

| A. | 1 | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{4}{3}$或2 |
5.已知向量$\overrightarrow{a}$=(2,m),$\overrightarrow{b}$=(-1,2),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{a}$在向量$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{b}$上的投影为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | -$\frac{\sqrt{10}}{2}$ | C. | -$\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{10}}{2}$ |
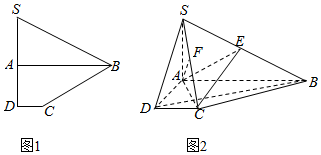 如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.
如图(1)所示,已知四边形SBCD是由直角△SAB和直角梯形ABCD拼接而成的,其中∠SAB=∠SDC=90°,且点A为线段SD的中点,AD=2DC=1,AB=SD,现将△SAB沿AB进行翻折,使得二面角S-AB-C的大小为90°,得到的图形如图(2)所示,连接SC,点E、F分别在线段SB、SC上.