题目内容
14.已知函数f(x)=|x+2|+|x-m|.(1)当m=6时,解不等式f(x)≥12;
(2)已知a>0,b>0,且$\frac{1}{a}$+$\frac{1}{b}$=$\sqrt{ab}$,若对于?a,b∈R*,?x0使f(x0)≤ab成立,求m的取值范围.
分析 (1)利用绝对值的意义,分类讨论,即可解不等式;
(2)求出ab≥2,f(x)min,即可求m的取值范围.
解答 解:(1)当m=6时,|x+2|+|x-6|≥12,
x<-2时,不等式化为-x-2-x+6≥12,∴x≤-4,此时x≤-4;
-2<x<6时,不等式化为x+2-x+6≥12,无解;
x≥6时,不等式化为x+2+x-6≥12,∴x≥8,此时x≥8;
综上所述,不等式的解集为{x|x≤-4或x≥8};
(2)a>0,b>0,且$\frac{1}{a}$+$\frac{1}{b}$=$\sqrt{ab}$≥2$\sqrt{\frac{1}{ab}}$,∴ab≥2(当且仅当a=b时取等号),
∵对于?a,b∈R*,?x0使f(x0)≤ab成立,
∴|2+m|≤2,
∴-4≤m≤0.
点评 本题考查不等式的解法,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
4.已知R为实数集,集合A={x|x2-2x≥0},B={x|x>1},则(∁RA)∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
5.△ABC中,角A,B,C的对边分别为a,b,c,若a=$\frac{\sqrt{6}}{2}$b,A=2B,则cosB 等于( )
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{6}}{5}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{6}}{3}$ |
2.若$\overrightarrow{AB}$$•\overrightarrow{AC}$=-1,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=1,则($\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$)•($\overrightarrow{AB}$+$\overrightarrow{AC}$)的值为( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{3}{2}$ |
9.如图,在△ABC中,N、P分别是AC、BN的中点,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AP}$=( )
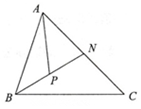

| A. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | B. | -$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | -$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ |
19.若双曲线E:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点为F(3,0),过F点的直线l与双曲线E交于A,B两点,且AB的中点为P(-3,-6),则E的方程为( )
| A. | $\frac{{x}^{2}}{5}$$-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{6}$$-\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{6}$=1 |
10.已知集合P={x∈N|1≤x≤5},集合Q={x∈R|x2-x-6<0},则P∩Q等于( )
| A. | {1,2,3} | B. | {1,2} | C. | [1,2] | D. | [1,3) |