题目内容
12.给出下列四个命题:①f(x)=sin(2x-$\frac{π}{4}$)的对称轴为x=$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z;
②若函数y=2cos(ax-$\frac{π}{3}$)的最小正周期是π,则a=2;
③函数f(x)=sinxcosx-1的最小值为-$\frac{3}{2}$;
④函数y=sin(x+$\frac{π}{4}$)在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数.
其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用正弦函数的性质以及它的图象特征,注意判断各个选项是否正确,从而得出结论.
解答 解:①对于f(x)=sin(2x-$\frac{π}{4}$),令2x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{3π}{8}$,
可得它的图象的对称轴为x=$\frac{kπ}{2}$+$\frac{3π}{8}$,k∈Z,故①正确.
②对于函数y=2cos(ax-$\frac{π}{3}$),它的最小正周期是|$\frac{2π}{a}$|=π,则a=±2,故②不正确.
③对于函数f(x)=sinxcosx-1=$\frac{1}{2}$sin2x-1,它的最小值为-$\frac{1}{2}$-1=-$\frac{3}{2}$,故③正确.
④对于函数y=sin(x+$\frac{π}{4}$),在[-$\frac{π}{2}$,$\frac{π}{2}$]上,x+$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3π}{4}$],故该函数不是增函数,故④错误,
故选:B.
点评 本题主要考查正弦函数的性质以及它的图象特征,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.设i是虚数单位,则复数z=i(3-4i)的虚部与模的和( )
| A. | 8 | B. | 9 | C. | 5+3i | D. | 5+4i |
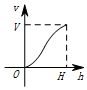
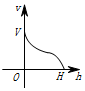
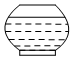 一个高为H,容积为V的鱼缸的轴截面如图所示,向鱼缸里注水,若鱼缸里的水面高度为h时,鱼缸里的水的体积为V',则函数V'=f(h)的大致图象可能是( )
一个高为H,容积为V的鱼缸的轴截面如图所示,向鱼缸里注水,若鱼缸里的水面高度为h时,鱼缸里的水的体积为V',则函数V'=f(h)的大致图象可能是( )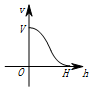
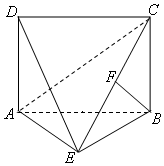 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.