题目内容
已知函数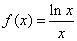 .
.
(Ⅰ)求函数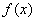 的单调区间及其极值;
的单调区间及其极值;
(Ⅱ)证明:对一切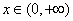 ,都有
,都有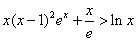 成立.
成立.
(Ⅰ)解: ,令
,令 ,得
,得 .
.
|
|
|
|
|
|
|
| 0 |
|
|
| 增 | 极大值 | 减 |
由上图表知:
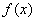 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 .
.
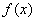 的极大值为
的极大值为 .
.
(Ⅱ)证明:对一切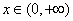 ,都有
,都有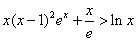 成立
成立
则有
由(Ⅰ)知,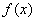 的最大值为
的最大值为 ,并且
,并且 成立,当且仅当
成立,当且仅当 时成立,
时成立,
函数 的最小值大于等于函数
的最小值大于等于函数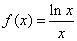 的最大值,但等号不能同时成立.
的最大值,但等号不能同时成立.
所以,对一切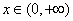 ,都有
,都有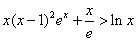 成立.
成立.

练习册系列答案
相关题目





 与椭圆
与椭圆 交于
交于 两点,设线段
两点,设线段 的中点为P.若直线
的中点为P.若直线 (
( 0),直线OP的斜率为
0),直线OP的斜率为 ,则
,则 D.
D.
 满足
满足 ,且
,且 ,
, . 则有穷数列{
. 则有穷数列{ }(
}(  )的前
)的前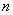 项和大于
项和大于 的概率是____________ .
的概率是____________ . 
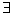 x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“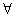 x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;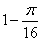 ;
;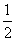 ,1)且与函数y=
,1)且与函数y=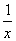 图象相切的直线方程是4x+y-3=0.
图象相切的直线方程是4x+y-3=0.  ,cosB=
,cosB= .若最长边为1,则最短边的长为 .
.若最长边为1,则最短边的长为 . ,则正四面体棱长为 。
,则正四面体棱长为 。 ,则
,则 .
.