“|x|+|y|≤1 是“x2+y2≤1 的( )条件．A．充分必要B．充分不必要C．必要不充分D．既不充分也不必要题目和参考答案——青夏教育精英家教网——

题目内容

7．“|x|+|y|≤1”是“x²+y²≤1”的（　　）条件．

	A．	充分必要		B．	充分不必要
	C．	必要不充分		D．	既不充分也不必要

分析根据不等式的性质以及充分必要条件的定义判断即可．

解答解：∵|x|+|y|≤1，
∴x²+y²+2|x||y|≤1，
∴x²+y²≤1，是充分条件，
而x²+y²≤1，推不出x²+y²+2|x||y|≤1，
也就推不出|x|+|y|≤1，不是必要条件，
故选：B．

点评本题考查了充分必要条件，考查不等式的性质，是一道基础题．

练习册系列答案

新语文阅读训练系列答案

秒杀口算题系列答案

口算题卡加应用题集训系列答案

中考1加1系列答案

鼎尖阅读系列答案

综合自测系列答案

走进重高培优测试系列答案

中考全程突破系列答案

名师金手指大试卷系列答案

标准课堂测试卷系列答案

相关题目

15．己知函数f（x）=（x+l）lnx-ax+a （a为正实数，且为常数）
（1）若f（x）在（0，+∞）上单调递增，求a的取值范围；
（2）若不等式（x-1）f（x）≥0恒成立，求a的取值范围．

18．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F₁，F₂，过点F₁作垂直于x轴的直线交椭圆C于M，N两点，若|MN|=3，且椭圆C上的离心率为$\frac{1}{2}$．
（I）求椭圆C的方程；
（Ⅱ）若直线AB的方程为3x+ty-3=0，且与椭圆C交于A，B两点，证明：$\frac{1}{|A{F}_{2}|}$+$\frac{1}{|B{F}_{2}|}$是定值．

15．设A={（x，y）|y=cos（arccosx）}，B={（x，y）|y=arccos（cosx）}，则A∩B=（　　）

	A．	{（x，y）\|y=x，-1≤x≤1}		B．	$\left\{{（x\;，\;\;y）\left\|{y=x\;，\;\;-\frac{1}{2}≤x≤\frac{1}{2}}\right.}\right\}$
	C．	{（x，y）y=x，0≤x≤1}		D．	{（x，y）\|y=x，0≤x≤π}

2．点P从点（-1，0）出发，沿单位圆x²+y²=1顺时针方向运动$\frac{π}{3}$弧长到达Q点，则Q点的坐标为（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．

12．若曲线 ${C_1}：y={x^2}$与曲线 ${C_2}：y=a{e^x}（a≠0）$存在唯一条公共切线，则a的取值范围为a＜0或a=$\frac{4}{{e}^{2}}$．

19．对于任意实数x，符号[x]表示x的整数部分，即[x]是不超过x的最大整数，例如[2]=2，[2.1]=2，[-2.2]=-3，这个函数[x]叫做“取整函数”，它在数学本身和生产实践中有广泛的应用．已知函数f（x）（x∈R）满足f（x）=f（2-x），且当x≥1时，f（x）=log₂x，那么[f（-16）]+[f（-15）]+…+[f（15）]+[f（16）]的值为84．

16．已知椭圆E的左、右焦点分别为F₁，F₂，过F₁且斜率为2的直线交椭圆E于P，Q两点，若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$，则椭圆E的离心率为（　　）

$\frac{{\sqrt{5}}}{3}$

$\frac{{\sqrt{2}}}{3}$

17．下列函数中，图象的一部分如右图所示的是（　　）

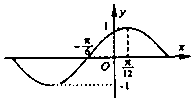
$y=sin（{x+\frac{π}{6}}）$

$y=cos（{2x-\frac{π}{6}}）$

$y=sin（{2x-\frac{π}{6}}）$

$y=cos（{4x-\frac{π}{3}}）$