题目内容
20．
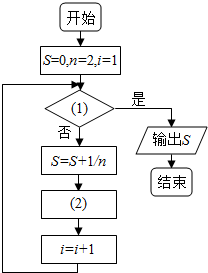如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图，则图中判断框内（1）处和执行框中的（2）处应填的语句是（ ）| A． | i＞1008，n=n+2 | B． | i≤1008，n=n+2 | C． | i＞2016，n=n+1 | D． | i＞2016，n=n+2 |
分析 根据算法的功能确定跳出循环的i值，可得判断框内的条件，根据n值的出现规律可得执行框②的执行式子．
解答 解：∵算法的功能是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值，
∴终止程序运行的n值为2018，i值为1009，
∴判断框的条件为i＞1008或i≥1009；
根据n值的规律得：执行框②应为n=n+2，
故选：A．
点评 本题考查了循环结构的程序框图，根据算法的功能确定跳出循环的i值及n值的出现规律是解答本题的关键，属于基础题．
练习册系列答案
相关题目
11．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左右顶点分别为A、B，左右焦点分别为F1、F2，若|AF1|，|F1F2|，|F1B|成等差数列，则此椭圆的离心率为（ ）
| A． | $\sqrt{5}-2$ | B． | $\frac{{\sqrt{5}}}{5}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
8．已知焦点在x轴上的椭圆过点A（-3，0），且离心率e=$\frac{{\sqrt{5}}}{3}$，则椭圆的标准方程是（ ）
| A． | $\frac{x^2}{9}+\frac{y^2}{{\frac{81}{4}}}$=1 | B． | $\frac{x^2}{4}+\frac{y^2}{9}$=1 | C． | $\frac{x^2}{{\frac{81}{4}}}+\frac{y^2}{9}$=1 | D． | $\frac{x^2}{9}+\frac{y^2}{4}$=1 |
9．从装有2个红球和2个白球的袋内任取两球，下列每对事件中是互斥事件的是（ ）
| A． | 至少有一个白球；都是白球 | B． | 恰好有一个白球；恰好有两个白球 | ||
| C． | 至少有一个白球；至少有一个红球 | D． | 至多有一个白球；都是红球 |