题目内容
5.已知变量x,y满足线性约束条件$\left\{\begin{array}{l}{4x+3y-25≤0}\\{x-4y+8≤0}\\{x-1≥0}\end{array}\right.$,若线性目标函数z=ax-y(a>1)的最大值为5,则实数a的值为2.分析 画出满足条件的平面区域,求出A的坐标,由z=ax-y得:y=ax-z,结合函数的图象显然直线y=ax-z过A(4,3)时,z最大,求出a的值即可.
解答 解:画出满足条件的平面区域,如图示: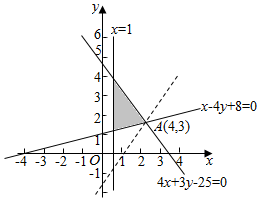 ,
,
由$\left\{\begin{array}{l}{4x+3y-25=0}\\{x-4y+8=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
由z=ax-y得:y=ax-z,
显然直线y=ax-z过A(4,3)时,z最大,
此时,5=4a-3,解得:z=2,
故答案为:2.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
16.已知函数$f(x)=2\sqrt{3}sin(3ωx+\frac{π}{3})\;(ω>0)$,若f(x+θ)是周期为2π的偶函数,则θ的一个可能值是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{7}{6}π$ | C. | π | D. | $\frac{5}{6}π$ |
13.已知椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的左、右焦点分别为F1、F2,点A在椭圆上,且|AF2|=6,则△AF1F2的面积是( )
| A. | 48 | B. | 40 | C. | 32 | D. | 24 |
20.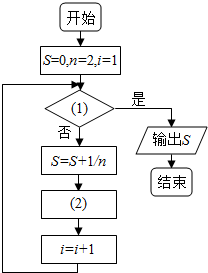 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )| A. | i>1008,n=n+2 | B. | i≤1008,n=n+2 | C. | i>2016,n=n+1 | D. | i>2016,n=n+2 |
10.在△ABC中,角A,B,C所对的边分别为a,b,c,若b=2$\sqrt{3}$.B=120°,C=30°,则a=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
14.函数f(x)=$\frac{\sqrt{2-x}}{1-lo{g}_{2}x}$的定义域为( )
| A. | (0,2] | B. | (0,2) | C. | (-2,2) | D. | [-2,2] |