题目内容
8.已知焦点在x轴上的椭圆过点A(-3,0),且离心率e=$\frac{{\sqrt{5}}}{3}$,则椭圆的标准方程是( )| A. | $\frac{x^2}{9}+\frac{y^2}{{\frac{81}{4}}}$=1 | B. | $\frac{x^2}{4}+\frac{y^2}{9}$=1 | C. | $\frac{x^2}{{\frac{81}{4}}}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{9}+\frac{y^2}{4}$=1 |
分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得a=3,由离心率公式和a,b,c的关系,可得b,进而得到椭圆方程.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得a=3,e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,
可得c=$\sqrt{5}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{9-5}$=2,
则椭圆方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1.
故选:D.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质及离心率公式和a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.一个样本的数据在60左右波动,各个数据都减去60后得到一组新数据,算得其平均数是6,则这个样本的平均数是( )
| A. | 6.6 | B. | 6 | C. | 66 | D. | 60 |
19.已知点M(-$\sqrt{3}$,0),N($\sqrt{3}$,0),若椭圆C:$\frac{{x}^{2}}{a}$+y2=1存在点P使|PM|-|PN|=2$\sqrt{2}$,则a的取值范围是( )
| A. | (0,1) | B. | (1,+∞) | C. | [2,+∞) | D. | [$\sqrt{2}$,+∞) |
16.已知函数$f(x)=2\sqrt{3}sin(3ωx+\frac{π}{3})\;(ω>0)$,若f(x+θ)是周期为2π的偶函数,则θ的一个可能值是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{7}{6}π$ | C. | π | D. | $\frac{5}{6}π$ |
3.将${({1-\frac{1}{x^2}})^n}(n∈{N_+})$的展开式中x-4的系数记为an,则$\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{{{a_{2016}}}}$等于( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | 2015 | D. | 2016 |
13.已知椭圆$\frac{{x}^{2}}{49}$+$\frac{{y}^{2}}{24}$=1的左、右焦点分别为F1、F2,点A在椭圆上,且|AF2|=6,则△AF1F2的面积是( )
| A. | 48 | B. | 40 | C. | 32 | D. | 24 |
20.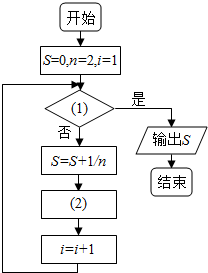 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )| A. | i>1008,n=n+2 | B. | i≤1008,n=n+2 | C. | i>2016,n=n+1 | D. | i>2016,n=n+2 |
18.已知函数f(x)=sin(2x+φ)+cos(2x+φ)的图象与函数$g(x)=\sqrt{2}sin({2x+\frac{π}{3}})$的图象关于y轴对称,则φ的值可以为( )
| A. | $-\frac{7π}{12}$ | B. | $-\frac{5π}{12}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |