题目内容
9.从装有2个红球和2个白球的袋内任取两球,下列每对事件中是互斥事件的是( )| A. | 至少有一个白球;都是白球 | B. | 恰好有一个白球;恰好有两个白球 | ||
| C. | 至少有一个白球;至少有一个红球 | D. | 至多有一个白球;都是红球 |
分析 利用互斥事件的定义求解.
解答 解:从装有2个红球和2个白球的袋内任取两球,
在A中,至少有一个白球和都是白球两个事件能同时发生,不是互斥事件,故A错误;
在B中,恰好有一个白球和恰好有两个白球两个事件不能同时发生,是互斥事件,故B正确;
在C中,至少有一个白球和至少有一个红球能够同时发生,不是互斥事件,故C错误;
在D中,至多有一个白球和都是红球两个事件能够同时发生,不是互斥事件,故D错误.
故选:B.
点评 本题考查互斥事件的求法,是基础题,解题时要认真审题,注意互斥事件的定义的合理运用.

练习册系列答案
相关题目
19.已知点M(-$\sqrt{3}$,0),N($\sqrt{3}$,0),若椭圆C:$\frac{{x}^{2}}{a}$+y2=1存在点P使|PM|-|PN|=2$\sqrt{2}$,则a的取值范围是( )
| A. | (0,1) | B. | (1,+∞) | C. | [2,+∞) | D. | [$\sqrt{2}$,+∞) |
20.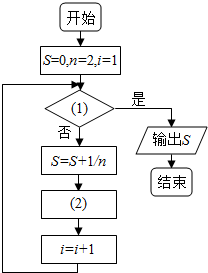 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )| A. | i>1008,n=n+2 | B. | i≤1008,n=n+2 | C. | i>2016,n=n+1 | D. | i>2016,n=n+2 |
4.已知复数Z满足Z•(1+i)=2i,则Z是( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
14.函数f(x)=$\frac{\sqrt{2-x}}{1-lo{g}_{2}x}$的定义域为( )
| A. | (0,2] | B. | (0,2) | C. | (-2,2) | D. | [-2,2] |
18.已知函数f(x)=sin(2x+φ)+cos(2x+φ)的图象与函数$g(x)=\sqrt{2}sin({2x+\frac{π}{3}})$的图象关于y轴对称,则φ的值可以为( )
| A. | $-\frac{7π}{12}$ | B. | $-\frac{5π}{12}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
19.若关于x的不等式(mx-1)(x-2)>0的解集为{x|$\frac{1}{m}$<x<2},则m的取值范围是( )
| A. | m>0 | B. | 0<m<2 | C. | m>$\frac{1}{2}$ | D. | m<0 |