题目内容
15.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c=$\sqrt{2}$b,过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.(1)求椭圆C的方程;
(2)若直线l1的斜率为-1,求△PMN的面积.
分析 (1)由题意推导出$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}$=1,且c2=2b2,再由a,b,c之间的关系,能求出椭圆C的方程.
(2)由于直线l1的斜率已确定,则可由其与椭圆联立方程组,求出点M的坐标,因两直线垂直,当k≠0时,用$-\frac{1}{k}$代替k,进而求出点N的坐标,得M(-2,0),N(1,1),再由两点意距离公式能求出△PMN的面积.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c=$\sqrt{2}$b,
过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N,
∴$\left\{\begin{array}{l}{{c}^{2}=2{b}^{2}}\\{\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得b2=$\frac{4}{3}$,a2=4.
∴椭圆方程为:$\frac{{x}^{2}}{4}+\frac{3{y}^{2}}{4}$=1.
(2)设l1方程为y+1=k(x+1),
联立$\left\{\begin{array}{l}{y=kx+k-1}\\{{x}^{2}+3{y}^{2}=4}\end{array}\right.$,
消去y得(1+3k2)x2+6k(k-1)x+3(k-1)2-4=0.
∵P(-1,1),解得M($\frac{-3{k}^{2}+6k+1}{1+3{k}^{2}}$,$\frac{3{k}^{2}+2k-1}{1+3{k}^{2}}$).
当k≠0时,用-$\frac{1}{k}$代替k,得N($\frac{{k}^{2}-6k-3}{3+{k}^{2}}$,$\frac{-{k}^{2}-2k+3}{3+{k}^{2}}$),
将k=1代入,得M(-2,0),N(1,1),
∵P(-1,-1),∴PM=$\sqrt{2}$,PN=2$\sqrt{2}$,
∴△PMN的面积为$\frac{1}{2}×\sqrt{2}×2\sqrt{2}$=2.
点评 本题考查椭圆方程的求法,考查三角形面积的求法,考查直线方程的求法,解题时要认真审题,注意点差法的合理运用.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | $\frac{2015}{2016}$ | B. | $\frac{2015}{1008}$ | C. | 2015 | D. | 2016 |
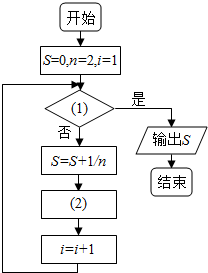 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+…+\frac{1}{2016}$的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是( )| A. | i>1008,n=n+2 | B. | i≤1008,n=n+2 | C. | i>2016,n=n+1 | D. | i>2016,n=n+2 |
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
| A. | 135° | B. | 120° | C. | 60° | D. | 45° |