题目内容
20.直线3x-4y-5=0的倾斜角的大小为arctan$\frac{3}{4}$(结果用反三角函数值表示)分析 根据所给的直线3x-4y-5=0,得到直线的斜率时$\frac{3}{4}$,直线的斜率是倾斜角的正切,得到tanα=$\frac{3}{4}$,α∈[0,π],根据倾斜角的范围和正切的反三角函数的值域确定结果.
解答 解:∵直线3x-4y-5=0,
∴直线的斜率时$\frac{3}{4}$,
直线的斜率是倾斜角的正切,
∴tanα=$\frac{3}{4}$,α∈[0,π],
∴α=arctan$\frac{3}{4}$,
故答案为:arctan$\frac{3}{4}$.
点评 本题考查反三角函数的应用及直线的倾斜角与斜率的关系,本题解题的关键是理解反三角函数的值域和倾斜角的范围,本题是一个基础题.

练习册系列答案
相关题目
10.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的两个焦点分别为F1,F2,若椭圆上存在点P使得∠F1PF2是钝角,则椭圆离心率的取值范围是( )
| A. | $(0,\frac{{\sqrt{2}}}{2})$ | B. | $(\frac{{\sqrt{2}}}{2},1)$ | C. | $(0,\frac{1}{2})$ | D. | $(\frac{1}{2},1)$ |
11.化简$\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{AD}$等于( )
| A. | $\overrightarrow{CD}$ | B. | $\overrightarrow{DC}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CB}$ |
12.已知抛物线y2=4x的准线l与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)相切,且l与该双曲线的渐近线相交于A、B两点,若△ABO(O为原点)为钝角三角形,则双曲线的离心率的取值范围为( )
| A. | ($\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
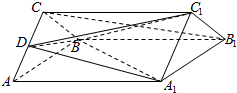 如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D
如图,在三棱柱ABC-A1B1C1中,棱AC的中点为D 如图,已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线为l1、l2.过椭圆C的右焦点F作直线l,使l丄l1.设直线l与椭圆C的两个交点由上至下依次为A,B,直线l与直线l2交于P点.
如图,已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线为l1、l2.过椭圆C的右焦点F作直线l,使l丄l1.设直线l与椭圆C的两个交点由上至下依次为A,B,直线l与直线l2交于P点.