题目内容
(1)甲盒中有红,黑,白三种颜色的球各3个,乙盒子中有黄,黑,白三种颜色的球各2个,从两个盒子中各取1个球,求取出的两个球是不同颜色的概率.
(2)在单位圆的圆周上随机取三点A、B、C,求△ABC是锐角三角形的概率.
(2)在单位圆的圆周上随机取三点A、B、C,求△ABC是锐角三角形的概率.
考点:几何概型
专题:计算题,概率与统计
分析:(1)设A=“取出的两球是相同颜色”,B=“取出的两球是不同颜色”,进而分析可得取出的两球是相同颜色,则两球的颜色均为黑色或白色,易得其情况数目,由等可能事件的概率可得事件A的概率,由对立事件的概率性质,可得答案;
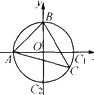
(2)建立平面直角坐标系,A、B、C1、C2为单位圆与坐标轴的交点,当C点在劣弧C1C2上运动时,△ABC即为锐角三角形,即可得出结论.
(2)建立平面直角坐标系,A、B、C1、C2为单位圆与坐标轴的交点,当C点在劣弧C1C2上运动时,△ABC即为锐角三角形,即可得出结论.
解答:
 解:(1)设A=“取出的两球是相同颜色”,B=“取出的两球是不同颜色”,则
解:(1)设A=“取出的两球是相同颜色”,B=“取出的两球是不同颜色”,则
事件A的概率为:P(A)=
=
.
由于事件A与事件B是对立事件,所以事件B的概率为:P(B)=1-P(A)=1-
=
(2)如图所示建立平面直角坐标系,A、B、C1、C2为单位圆与坐标轴的交点,当△ABC为锐角三角形,记为事件A.则当C点在劣弧C1C2上运动时,△ABC即为锐角三角形,即事件A发生,所以P(A)=
=
.
 解:(1)设A=“取出的两球是相同颜色”,B=“取出的两球是不同颜色”,则
解:(1)设A=“取出的两球是相同颜色”,B=“取出的两球是不同颜色”,则事件A的概率为:P(A)=
| 3×2+3×2 |
| 9×6 |
| 2 |
| 9 |
由于事件A与事件B是对立事件,所以事件B的概率为:P(B)=1-P(A)=1-
| 2 |
| 9 |
| 7 |
| 9 |
(2)如图所示建立平面直角坐标系,A、B、C1、C2为单位圆与坐标轴的交点,当△ABC为锐角三角形,记为事件A.则当C点在劣弧C1C2上运动时,△ABC即为锐角三角形,即事件A发生,所以P(A)=
| ||
| 2π |
| 1 |
| 4 |
点评:本题考查等可能事件的概率,(1)中颜色不同情况较多,可以利用对立事件的概率性质,先求“取出的两球是相同颜色”的概率,再求出“取出的两球是不同颜色”的概率.

练习册系列答案
相关题目
已知
+
=(-1,5),
-
=(5,-3),则
,
的坐标正确的是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若(x-
)9的展开式中x3的系数是-84,则a=( )
| a |
| x |
| A、2 | B、-2 | C、1 | D、-1 |
已知变量x,y满足约束条件
,则z=3x+y的最大值为( )
|
| A、12 | B、11 | C、3 | D、-1 |
如图,AB是⊙O的直径,P在AB的延长线上,PC切⊙O于C,PC=
,BP=1,则⊙O的半径为( )

| 3 |

A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|