题目内容
若等腰梯形ABCD中,AB∥CD,AB=3,BC=
,∠ABC=45°,则
•
的值为 .
| 2 |
| AC |
| BD |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据已知条件及向量的加法:
•
=(
+
)•(
+
)=-3+
•
,而要求
•
只需知道向量
,
的夹角,而通过过D作BC的平行线,根据已知的角即可求出
,
的夹角,这样即可求得答案.
| AC |
| BD |
| AB |
| BC |
| BA |
| AD |
| BC |
| AD |
| BC |
| AD |
| BC |
| AD |
| BC |
| AD |
解答:
解:如图,
•
=(
+
)•(
+
)=-
2+
•
+
•
+
•
 =-9+3+3+
=-9+3+3+
•
;
过D作DE∥BC,根据已知条件,∠ADC=135°,∠EDC=45°;
∴∠ADE=90°;
∴
•
=0;
∴
•
=-3.
故答案为:-3.
| AC |
| BD |
| AB |
| BC |
| BA |
| AD |
| AB |
| AB |
| AD |
| BC |
| BA |
| BC |
| AD |
 =-9+3+3+
=-9+3+3+| BC |
| AD |
过D作DE∥BC,根据已知条件,∠ADC=135°,∠EDC=45°;
∴∠ADE=90°;
∴
| BC |
| AD |
∴
| AC |
| BD |
故答案为:-3.
点评:考查向量加法的几何意义,向量数量积的计算公式,以及等腰梯形的边角关系.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知函数f(x)=
sin2xsinφ+cos2xcosφ-
sin(
+φ)(0<φ<π),将凼数f(x)的图象向左移
个单位后关于y轴对称,则φ等于( )
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,则函数g(x)=f(x)-x在区间[-5,5]上的零点之和为( )
|
| A、15 | B、16 | C、30 | D、32 |
过抛物线y2=2px的焦点F作直线交抛物线于M,N两点,弦MN的垂直平分线交x轴于点H,若|MN|=40,则|HF|=( )
| A、14 | B、16 | C、18 | D、20 |
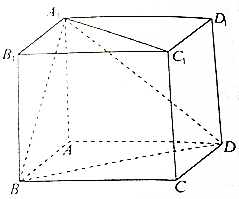 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: