题目内容
下列函数中,既是奇函数又是定义域上的增函数的是( )
| A、y=x+1 | ||
| B、y=ex-e-x | ||
C、y=
| ||
D、y=x
|
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:抓住题目要求,判断给定的函数既是奇函数又是定义域上的增函数,进行逐个判断即可.
解答:
解:选项A中函数为非奇非偶函数,不符合题意;
选项D中函数为非奇非偶函数,不符合题意;
选项C中,该函数的单调增区间为(-∞,0),(0,+∞),不符合题目要求;
选项B中,函数y=ex-e-x
该函数的定义域为R,
设y=f(x),则f(-x)=e-x-ex=-f(x)
所以该函数为奇函数,
任设x1,x2∈R x1<x2,
f(x1)-f(x2)=ex1-ex2+
-
<0,
所以该函数为增函数,
满足条件,
故选B.
选项D中函数为非奇非偶函数,不符合题意;
选项C中,该函数的单调增区间为(-∞,0),(0,+∞),不符合题目要求;
选项B中,函数y=ex-e-x
该函数的定义域为R,
设y=f(x),则f(-x)=e-x-ex=-f(x)
所以该函数为奇函数,
任设x1,x2∈R x1<x2,
f(x1)-f(x2)=ex1-ex2+
| 1 |
| ex1 |
| 1 |
| ex2 |
所以该函数为增函数,
满足条件,
故选B.
点评:本题重点考查函数的单调性与奇偶性的及其运用,函数具备奇偶性的前提为给定函数的定义域关于原点对称;函数的单调性的判断可以结合图象,也可以借助于定义求解.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
已知定义在R上的可导函数y=f(x)的导函数为f′(x),满足f(x)<f′(x),且f(0)=2,则不等式
>2的解集为( )
| f(x) |
| ex |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,2) |
| D、(2,+∞) |
正方体AC1中,则AD1与平面BB1D1D所成角为( )
| A、30° | B、60° |
| C、45° | D、90° |
已知a<b<c<d<0,且d=
,则a+d与b+c的大小关系是( )
| bc |
| a |
| A、a+d<b+c |
| B、a+d>b+c |
| C、a+d=b+c |
| D、以上三种情况都有可能 |
已知函数f(x+1)是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式x1f(x1)+x2f(x2)<x1f(x2)+x2f(x1)恒成立,则不等式f(1-x)<0的解集为( )
| A、(1,+∞) |
| B、(-∞,0) |
| C、(0,+∞) |
| D、(-∞,1) |
已知正方体的棱长为2,则外接球的表面积和体积( )
A、48π,32
| ||
B、48π,4
| ||
C、12π,4
| ||
D、12π,32
|
复数z=i(1-2i)(i为虚数单位)的共轭复数在复平面上的对应点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,△ABC中,∠C=90°,且AC=BC=4,点M满足
如图,△ABC中,∠C=90°,且AC=BC=4,点M满足| BM |
| MA |
| CM |
| CB |
| A、2 | B、3 | C、4 | D、6 |
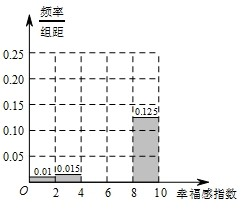 前不久央视记者就“你幸福吗?”采访了走在接头及工作岗位上的部分人员.人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.为了解某地区居民的幸福感,随机对该地区的男、女居民各500人进行了调查,调查数据如表所示:
前不久央视记者就“你幸福吗?”采访了走在接头及工作岗位上的部分人员.人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.为了解某地区居民的幸福感,随机对该地区的男、女居民各500人进行了调查,调查数据如表所示: