题目内容
若cosx+cosy=
,sinx-siny=
,则cos(x+y)= .
| 1 |
| 2 |
| 1 |
| 3 |
考点:两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:直接通过两个表达式平方,相加,即可通过两角和的余弦函数求解即可.
解答:
解:sinx-siny=
,cosx+cosy=
,
可得(sinx-siny)2=
,(cosx+cosy)2=
,
即sin2x-2sinxsiny+sin2y=
,cos2x+2cosxcosy+cos2y=
,
两式相加,可得:1+2(cosxcosy-sinxsiny)+1=
,
cosxcosy-sinxsiny=-
,
即cos(x+y)=-
.
故答案为:-
.
| 1 |
| 3 |
| 1 |
| 2 |
可得(sinx-siny)2=
| 1 |
| 9 |
| 1 |
| 4 |
即sin2x-2sinxsiny+sin2y=
| 1 |
| 9 |
| 1 |
| 4 |
两式相加,可得:1+2(cosxcosy-sinxsiny)+1=
| 13 |
| 36 |
cosxcosy-sinxsiny=-
| 59 |
| 72 |
即cos(x+y)=-
| 59 |
| 72 |
故答案为:-
| 59 |
| 72 |
点评:本题考查两角和的余弦函数以及同角三角函数的基本关系式的应用,考查平方法和计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知命题p:?x∈R,x+2>2x,命题q:?x∈R,x2>0,则( )
| A、命题p∨q是假命题 |
| B、命题p∧(¬q)是真命题 |
| C、命题p∧q是真命题 |
| D、命题p∨(¬q)是假命题 |
已知f(x)=cos x,则f′(
)等于( )
| 5π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知点(3,M)到直线x+
y-4=0的距离等于1,则m等于?( )
| 3 |
A、
| ||||||
B、-
| ||||||
C、-
| ||||||
D、
|
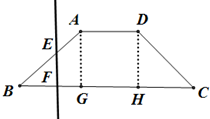 如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2
如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2