题目内容
20．已知复数z=cosθ+isinθ．（1）求z2和z3；
（2）利用归纳推理推测zn的表达式．
分析 （1）利用复数的运算法则、倍角公式即可得出；
（2）利用（1）通过归纳推理推测可得：zn的表达式．
解答 解：（1）∵z=cosθ+isinθ，
∴z2=（cosθ+isinθ）2=cos2θ-sin2θ+2sinθcosθ=cos2θ+isin2θ．
∴z3=（cosθ+isinθ）2（cosθ+isinθ）=（cos2θ+isin2θ）（cosθ+isinθ）
=（cos2θcosθ-sin2θsinθ）+i（cos2θsinθ+sin2θcosθ）=cos3θ+isin3θ．
（2）由z=cosθ+isinθ，z2=cos2θ+isin2θ，z3=cos3θ+isin3θ，
进行归纳推理可知zn=cosnθ+isinnθ．
点评 本题考查了复数的运算法则、倍角公式、归纳推理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
10．已知i是虚数单位，且$z={（\frac{1-i}{1+i}）^{2016}}$+i的共轭复数为$\overline{z}$，则z$•\overline{z}$等于（ ）
| A． | 2 | B． | 1 | C． | 0 | D． | -l |
11．已知向量$\overrightarrow{a}$=（4cosx，$\frac{1}{3}$），$\overrightarrow{b}$=（sin（x+$\frac{π}{6}$），-1），且$\overrightarrow{a}•\overrightarrow{b}$=0，则sin（2x+$\frac{7π}{6}$）=（ ）
| A． | -$\frac{2\sqrt{2}}{3}$ | B． | -$\frac{1}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{1}{3}$ |
8．集合A={x|-1≤x≤1}，B={x|x∈Z}，则A∩B=（ ）
| A． | （-1，1） | B． | {0，1} | C． | {-1，0，1} | D． | {1} |
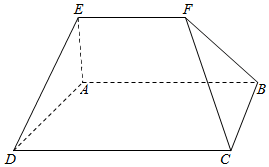如图，用四种不同颜色的灯泡安装在图中的A，B，C，D，E，F六个点，要求每个点安装一个灯袍，且图中每条线段两个端点的灯泡颜色不同，则不同的安装方法共有多少种？