题目内容
将二次函数y=-x2的图象按
=(h,1)平移,使得平移后的图象与函数y=x2-x-2的图象有两个不同的公共点A和B,且向量
+
(O为原点)与向量
=(2,-4)共线,求平移后的图象的解析式.
| a |
| OA |
| OB |
| b |
考点:二次函数的性质
专题:平面向量及应用
分析:根据向量平移可以设所求解析式为y=-(x-h)2+1,所以联立解析式y=x2-x-2便可得到2x2-(2h+1)x+h2-3=0,设A(x1,y1),B(x2,y2),根据韦达定理便得x1+x2=
,x1x2=
,并且能得到y1+y2=-
,这样便得到
+
=(
,-
),而根据向量
+
和向量
共线,即知存在实数,并且知道该实数为
,使得
+
=
,带入坐标即可求得h.
| 2h+1 |
| 2 |
| h2-3 |
| 2 |
| 5 |
| 4 |
| OA |
| OB |
| 2h+1 |
| 2 |
| 5 |
| 4 |
| OA |
| OB |
| b |
| 5 |
| 16 |
| OA |
| OB |
| 5 |
| 16 |
| b |
解答:
解:设所求解析式为y-1=-(x-h)2;
由
得,2x2-(2h+1)x+h2-3=0;
设A(x1,y1),B(x2,y2),则:
x1+x2=
,x1x2=
;
∴y1+y2=x12-x1-2+x22-x2-2=(x1+x2)2-2x1x2-(x1+x2)-4=(
)2-2•
-
-4=-
;
∴
+
=(x1+x2,y1+y2)=(
,-
);
∵
+
和
=(2,-4)共线;
∴(
,-
)=
(2,-4);
∴
=
;
∴h=
;
∴所求解析式为y=(x-
)2+1=x2-
x+
;
即y=x2-
x+
.
由
|
设A(x1,y1),B(x2,y2),则:
x1+x2=
| 2h+1 |
| 2 |
| h2-3 |
| 2 |
∴y1+y2=x12-x1-2+x22-x2-2=(x1+x2)2-2x1x2-(x1+x2)-4=(
| 2h+1 |
| 2 |
| h2-3 |
| 2 |
| 2h+1 |
| 2 |
| 5 |
| 4 |
∴
| OA |
| OB |
| 2h+1 |
| 2 |
| 5 |
| 4 |
∵
| OA |
| OB |
| b |
∴(
| 2h+1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 16 |
∴
| 2h+1 |
| 2 |
| 5 |
| 8 |
∴h=
| 1 |
| 8 |
∴所求解析式为y=(x-
| 1 |
| 8 |
| 1 |
| 4 |
| 65 |
| 64 |
即y=x2-
| 1 |
| 4 |
| 65 |
| 64 |
点评:考查向量平移的概念,及平移前后坐标的关系,韦达定理,共线向量基本定理,以及向量坐标的数乘运算.

练习册系列答案
相关题目
已知点P是抛物线y2=4x上一动点,则点P到点A(0,-2)的距离与到直线x=-1的距离的最小值是( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
 如图,在△ABC中,线段BE,CF交于点P,设向量
如图,在△ABC中,线段BE,CF交于点P,设向量| AB |
| a |
| AC |
| b |
| AP |
| c |
| AF |
| 2 |
| 3 |
| a |
| AE |
| 1 |
| 2 |
| b |
| c |
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
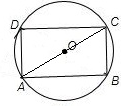 如图,长为4,宽为3的矩形ABCD的外接圆为圆O,在圆O内任取M,点M在△ABC内的概率是
如图,长为4,宽为3的矩形ABCD的外接圆为圆O,在圆O内任取M,点M在△ABC内的概率是