题目内容
求f(x)=1-2sin2x-2cosx的最值.
考点:三角函数的最值
专题:三角函数的求值
分析:先把函数转化为关于cosx的一元二次函数,进而根据二次函数的性质求得函数的最小值.
解答:
解:f(x)=1-2sin2x-2cosx=1-2+2cos2x-2cosx=2cos2x-2cosx-1=2(cosx-
)2-
,
∵-1≤cosx≤1,
∴当cosx=
时,函数取最小值,最小值为-
,
当cosx=-1时,函数取最大值为3.
| 1 |
| 2 |
| 3 |
| 2 |
∵-1≤cosx≤1,
∴当cosx=
| 1 |
| 2 |
| 3 |
| 2 |
当cosx=-1时,函数取最大值为3.
点评:本题主要考查了二次函数与余弦函数的性质相结合求最值.解题的关键是利用余弦函数的有界性将问题转化为二次函数闭区间上的最值求法.

练习册系列答案
相关题目
已知
、
是两个不平行的非零向量,并且
∥
,
∥
,则向量
等于( )
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
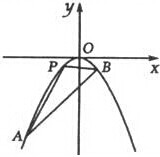 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,