题目内容
已知sin(2α+β)+2sinβ=0,求证:tanα=3tan(α+β).
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:把已知等式左边的角β变为(α+β)-α,右边的角2α+β变为(α+β)+α,然后左右两边分别利用两角和与差的正弦函数公式化简,移项合并后,在等式两边同时除以cosαcos(α+β),利用同角三角函数间的基本关系变形可得证.
解答:
证明:将条件化为:sin[(α+β)+α]+2sin[(α+β)-α]=0,
展开得:sin(α+β)cosα+cos(α+β)sinα+2sin(α+β)cosα-2cos(α+β)sinα=0,
即:3sin(α+β)cosα=cos(α+β)sinα,
由cos(α+β)cosα≠0,两边同除以cos(α+β)cosα,
可得:tanα=3tan(α+β)=.(12分)
展开得:sin(α+β)cosα+cos(α+β)sinα+2sin(α+β)cosα-2cos(α+β)sinα=0,
即:3sin(α+β)cosα=cos(α+β)sinα,
由cos(α+β)cosα≠0,两边同除以cos(α+β)cosα,
可得:tanα=3tan(α+β)=.(12分)
点评:此题考查了三角函数的恒等式的证明,用到的知识有:两角和与差的正弦函数公式,以及同角三角函数间的基本关系,把已知等式左右两边的角度灵活变换是本题的突破点.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
若不等式x2-
x≥0对任意实数x都成立,则实数a的取值是( )
| a |
| A、{0} | B、{0,1} |
| C、(0,1) | D、[0,+∞) |
已知
、
是两个不平行的非零向量,并且
∥
,
∥
,则向量
等于( )
| a |
| b |
| a |
| c |
| b |
| c |
| c |
A、
| ||
B、
| ||
C、
| ||
D、
|
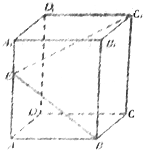 长方体ABCD-A1B1C1D1的底面是边长为a的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值为( )
长方体ABCD-A1B1C1D1的底面是边长为a的正方形,若在侧棱AA1上至少存在一点E,使得∠C1EB=90°,则侧棱AA1的长的最小值为( )