题目内容

已知函数f（x）=ax2-|x|+2a-1（a为常数）．
（1）若a=1，作出函数f（x）的图象；
（2）若函数f（x）在区间（1，+∞）上是增函数，求a的取值范围．
考点：二次函数的性质,函数单调性的性质
专题：函数的性质及应用
分析：（1）将a=1代入，结合二次函数的图象和性质，可作出函数f（x）的图象；
（2）当x＞0时，函数f（x）=ax2-x+2a-1，若函数f（x）在区间（1，+∞）上是增函数，则
a＞0
1
2a
≤1
，解得a的取值范围．
解答： 解：（1）当a=1时，f（x）=x2-|x|+1，
其中图象如下图所示：

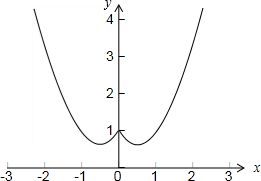
（2）当x＞0时，函数f（x）=ax2-x+2a-1，
若函数f（x）在区间（1，+∞）上是增函数，
则
a＞0
1
2a
≤1
，
解得：a∈[
1
2
，+∞），
故a的取值范围是[
1
2
，+∞）．
点评：本题考查的知识点是二次函数的图象和性质，函数单调性的性质，难度不大，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=x2+2x-a，方程f（f（x））=0有不等的4个实根，求a的取值范围．
给出定义：若m-
1
2
＜x≤m+
1
2
（其中m为整数），则m叫做离实数x最近的整数，记作（x）=m，在此基础上给出下列关于函数f（x）=log
1
2
|x-{x}|的四个命题：
①函数y=f（x）的定义域为R，值域为[1，+∞）；
②函数y=f（x）在（-
1
2
，0）上是增函数；
③函数y=f（x）是周期函数，最小正周期为1；
④函数y=f（x）的图象关于直线x=
k
2
（k∈Z）对称．
其中正确命题的序号是
 
．
己知f（x+y）=f（x）+f（y），且f（1）=2，则f（1）+f（2）+…+f（n）=
 
．
已知函数f（x）=|x2-2ax+b|（x∈R）．给出下列四个命题：
（1）f（x）必是偶函数；
（2）当f（0）=f（2）时，f（x）的图象必关于直线 x=1对称；
（3）若a2-b≤0时，则f（x）在区间[a，+∞）上是增函数；
（4）f（x）有最大值|a2-b|；
其中所有真命题的序号是
 
．
求经过点（5，10）且与原点的距离为5的直线方程．
已知函数f（x）=x+
a
x
（a＞0）
（1）判断它的奇偶性；
（2）求证：f（x）在（0，
a
）上是减函数．
将二次函数y=-x2的图象按
a
=（h，1）平移，使得平移后的图象与函数y=x2-x-2的图象有两个不同的公共点A和B，且向量
OA
+
OB
（O为原点）与向量
b
=（2，-4）共线，求平移后的图象的解析式．
已知函数f（x）=2x-
1
2|x|
．
（1）求f（-4）的值；
（2）若f（x）=2，求x的值；
（3）若2tf（2t）+mf（t）≥0对于t∈[1，2]恒成立，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网