题目内容
已知点P是抛物线y2=4x上一动点，则点P到点A（0，-2）的距离与到直线x=-1的距离的最小值是（ ）
A、
| ||
B、
| ||
| C、2 | ||
D、
|
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设A（0，-2），先求出焦点及准线方程，过P作PN垂直直线x=-1，有|PN|=|PF|，连接F、A，有|FA|≤|PA|+|PF|，从而只求|FA|．
解答：
解：设A（0，-2），由y2=4x得p=2，
=1，
所以抛物线的焦点为F（1，0），准线x=-1，
过P作PN垂直直线x=-1，根据抛物线的定义，
抛物线上一点到定直线的距离等于到焦点的距离，
所以有|PN|=|PF|，连接F、A，有|FA|≤|PA|+|PF|，
所以P为AF与抛物线的交点，点P到点A（0，-2）的距离与点P到直线X=-1的距
离之和的最小值为|FA|=
=
，
故选：A
| p |
| 2 |
所以抛物线的焦点为F（1，0），准线x=-1，
过P作PN垂直直线x=-1，根据抛物线的定义，
抛物线上一点到定直线的距离等于到焦点的距离，
所以有|PN|=|PF|，连接F、A，有|FA|≤|PA|+|PF|，
所以P为AF与抛物线的交点，点P到点A（0，-2）的距离与点P到直线X=-1的距
离之和的最小值为|FA|=
| 12+22 |
| 5 |
故选：A
点评：本题考查抛物线的定义及简单性质，考查数形结合思想，属中档题．
练习册系列答案
相关题目
若不等式x2-
x≥0对任意实数x都成立，则实数a的取值是（ ）
| a |
| A、{0} | B、{0，1} |
| C、（0，1） | D、[0，+∞） |
抛物线x2=-
y的准线方程是（ ）
| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、x=
| ||
D、x=
|
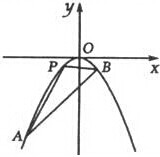如图，已知直线l：y=kx-2与抛物线C：x2=-2py（p＞0）交于A，B两点，O为坐标原点，