题目内容
已知抛物线C：y2=2px的焦点坐标为F（2，0），点A（6，3），若点M在抛物线C上，则|MA|+|MF|的最小值为 ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据抛物线方程及A点坐标可以推知A点在抛物线内，把抛物线上的点到焦点的距离转化为到抛物线的准线的距离，结合图象，易得过点A且与准线l垂直的直线与抛物线的交点即为所求，进而得到最小值．
解答：
解：抛物线C：y2=2px的焦点F为（2，0），准线方程为x=-2．
设P是抛物线上任意一点，l是抛物线的准线，
过P作PP1 ⊥L，垂足为P1，过A作AA1⊥l，垂足为A1，
且交抛物线于点M，
∴|PA|+|PF|=|PA|+|PP1|≥|AA1|=|MA|+|MA1|
=|MF|+|MA|，
此时MA+MF的最小值为6-（-2）=8．
故答案为：8．
解：抛物线C：y2=2px的焦点F为（2，0），准线方程为x=-2．设P是抛物线上任意一点，l是抛物线的准线，
过P作PP1 ⊥L，垂足为P1，过A作AA1⊥l，垂足为A1，
且交抛物线于点M，
∴|PA|+|PF|=|PA|+|PP1|≥|AA1|=|MA|+|MA1|
=|MF|+|MA|，
此时MA+MF的最小值为6-（-2）=8．
故答案为：8．
点评：本题主要考查了抛物线的定义，充分利用了抛物线上的点到准线的距离与点到焦点的距离相等这一特性，运用了转化思想和数形结合思想．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图，四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，BC=PB=PC，PO⊥AD，O为BC的中点．
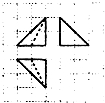如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的各个面中最大面的面积为（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|