题目内容
某售货员负责在甲、乙、丙三个柜台上售货，如果在某一小时内各柜台不需要售货员照顾的概率分别为0.9，0.8，0.7，假定各个柜台是否需要照顾相互之间没有影响，求这个小时内：
（1）只有丙柜台需要售货员照顾的概率？
（2）三个柜台至少有一个需要售货员照顾的概率？
（3）三个柜台至多有一个需要售货员照顾的概率？
（1）只有丙柜台需要售货员照顾的概率？
（2）三个柜台至少有一个需要售货员照顾的概率？
（3）三个柜台至多有一个需要售货员照顾的概率？
考点：概率的应用
专题：应用题,概率与统计
分析：利用相互对立事件、独立事件、对立的概率的计算公式，即可得出结论．
解答：
解：（1）只有丙柜台需要售货员照顾的概率为0.9×0.8×0.3=0.216；
（2）三个柜台至少有一个需要售货员照顾的概率为1-0.9×0.8×0.7=0.496；
（3）（1-0.9）（1-0.8）（1-0.7）+（1-0.9）×0.8×0.7+0.9×（1-0.8）×0.7+0.9×0.8×（1-0.7）=0.902．
（2）三个柜台至少有一个需要售货员照顾的概率为1-0.9×0.8×0.7=0.496；
（3）（1-0.9）（1-0.8）（1-0.7）+（1-0.9）×0.8×0.7+0.9×（1-0.8）×0.7+0.9×0.8×（1-0.7）=0.902．
点评：本题考查相互对立事件、独立事件、对立的概率的计算，概率问题经常涉及多种关系的事件组合，解题时要分清事件之间的关系．
练习册系列答案
相关题目
已知命题：若数列{an}为等差数列，且am=a，an=b（m≠n，m、n∈N+）则am+n=
；现已知等比数列{bn}（bn＞0，n∈N+），bm=a，bn=b，（m≠n，m、n∈N+）若类比上述结论，则可得到bm+n=（ ）
| bn-am |
| n-m |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
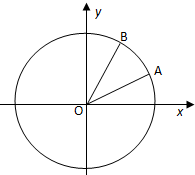如图，在平面直角坐标系xOy中，以Ox轴为始边，两个锐角α，β的终边分别与单位圆相交于A，B 两点．
某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．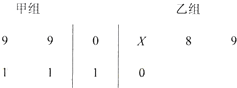
以下茎叶图记录了甲、乙两组各四名同学的植树棵数．乙组记录中有一个数据模糊，无法确认，在图中以X表示．