题目内容
3.中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(2,-1),则它的离心率为$\frac{\sqrt{5}}{2}$.分析 利用已知条件列出关系式求解即可.
解答 解:中心在原点,焦点在x轴上的双曲线的一条渐近线经过点(2,-1),
可得2b-a=0,即4c2-4a2=a2,
可得4c2=5a2
e=$\frac{\sqrt{5}}{2}$.
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
18.设复数z满足$\overline{z}$=|1-i|+i(i为虚数单位),则复数z为( )
| A. | $\sqrt{2}$-i | B. | $\sqrt{2}$+i | C. | 1 | D. | -1-2i |
15.曲线x2+(y-1)2=1(x≤0)上的点到直线x-y-1=0的距离最大值为a,最小值为b,则a-b的值是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$+1 | D. | $\sqrt{2}$-1 |
12.甲乙和其他4名同学合影留念,站成两排三列,且甲乙两人不在同一排也不在同一列,则这6名同学的站队方法有( )
| A. | 144种 | B. | 180种 | C. | 288种 | D. | 360种 |
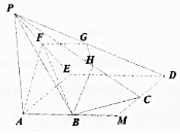 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.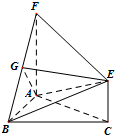 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF${\;}_{=}^{∥}$2CE,G是线段BF上一点,AB=AF=BC
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF${\;}_{=}^{∥}$2CE,G是线段BF上一点,AB=AF=BC