题目内容
13.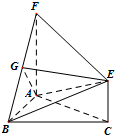 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF${\;}_{=}^{∥}$2CE,G是线段BF上一点,AB=AF=BC
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF${\;}_{=}^{∥}$2CE,G是线段BF上一点,AB=AF=BC(Ⅰ)若EG∥平面ABC,求$\frac{BG}{BF}$的值;
(Ⅱ)是否在线段BF上存在点G满足BF⊥平面AEG?请说明理由.
分析 (Ⅰ)由线面平行的性质定理可得过EG的平面与平面ABC交于CD,D在AB上,连接GD,CD,可得EG∥CD,根据线面平行的判定定理和性质定理,证明CE∥GD,可得四边形GDCE是平行四边形,进而得到G为BF的中点;
(Ⅱ)根据面面垂直的性质定理以及线面垂直的判定定理和性质定理,建立空间直角坐标系,求出F,B,C,E的坐标,运用向量的数量积的坐标表示,计算$\overrightarrow{BF}$•$\overrightarrow{AE}$,即可得到结论.
解答 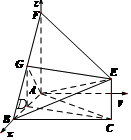 解:(Ⅰ)EG∥平面ABC,
解:(Ⅰ)EG∥平面ABC,
过EG的平面与平面ABC交于CD,D在AB上,
连接GD,CD,
由线面平行的性质定理可得EG∥CD,
又因为AF∥CE,AF=2CE,
CE?平面ABF,AF?平面ABF,
CE∥平面ABF,CE?平面CEGD,
可得CE∥GD,
则四边形GDCE是平行四边形,
即有AF∥GD,AF=2GD,
即G为BF的中点,
则$\frac{BG}{BF}$=$\frac{1}{2}$;
(Ⅱ)因为平面ABC⊥平面ACEF,平面ABC∩平面ACEF=AC,
且AF⊥AC,所以AF⊥平面ABC,
所以AF⊥AB,AF⊥BC,
因为BC⊥AB,所以BC⊥平面ABF.
如图,以A为原点,建立空间直角坐标系A-xyz.
设AB=AF=BC=2,
则F(0,0,2),B(2,0,0),C(2,2,0),E(2,2,1),
因为$\overrightarrow{BF}$•$\overrightarrow{AE}$=(-2,0,2)•(2,2,1)=-2×2+2=0×2+2×1=-2≠0,
所以BF与AE不垂直,
所以不存在点G满足BF⊥平面AEG.
点评 本题主要考查线面平行的判定和性质定理的运用,以及中位线定理的运用,线面垂直的存在性问题,建立空间直角坐标系,利用向量法是解决本题的关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案| A. | (-2,+∞) | B. | (-2,2) | C. | (-∞,-2) | D. | (-∞,+∞) |
| A. | 20% 369 | B. | 80% 369 | C. | 40% 360 | D. | 60% 365 |
| A. | (2,3] | B. | [2,3] | C. | (-∞,0)∪(0,2] | D. | (-∞,-1)∪(0,3] |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
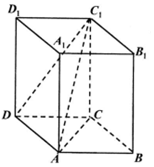 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.