题目内容
11.已知$f(x)=\frac{kx+b}{e^x}$.(1)若f(x)在x=0处的切线方程为y=x+1,求k与b的值;
(2)求$\int_0^1{\frac{x-1}{e^x}}{d_x}$.
分析 (1)根据导数的几何意义可得f(0)=1,f′(0)=1,列方程组解出即可;
(2)结合(1)中的导数可求得y=$\frac{x-1}{{e}^{x}}$的原函数,利用微积分基本定理计算定积分.
解答 解:(1)f′(x)=$\frac{k{e}^{x}-(kx+b){e}^{x}}{{e}^{2x}}$=$\frac{k-kx-b}{{e}^{x}}$.
∵f(x)在x=0处的切线方程为y=x+1,
∴$\left\{\begin{array}{l}{f(0)=1}\\{f′(0)=1}\end{array}\right.$,即$\left\{\begin{array}{l}{b=1}\\{k-b=1}\end{array}\right.$,
解得k=2,b=1.
(2)令$\frac{k-kx-b}{{e}^{x}}$=$\frac{x-1}{{e}^{x}}$得$\left\{\begin{array}{l}{-k=1}\\{k-b=-1}\end{array}\right.$,
解得k=-1,b=0,
∴($\frac{-x}{{e}^{x}}$)′=$\frac{x-1}{{e}^{x}}$,
∴$\int_0^1{\frac{x-1}{e^x}}{d_x}$=$\frac{-x}{{e}^{x}}$${|}_{0}^{1}$=-$\frac{1}{e}$.
点评 本题考查了导数的几何意义,微积分基本定理,属于中档题.

练习册系列答案
相关题目
19.执行下面的程序框图,输出S的值为( )


| A. | 8 | B. | 18 | C. | 26 | D. | 80 |
16.用半径为R的圆铁皮剪一个内接矩形,再以内接矩形的两边分别作为圆柱的高与底面半径,则圆柱的体积最大时,该圆铁皮面积与其内接矩形的面积比为( )
| A. | $\frac{3\sqrt{3}π}{8}$ | B. | $\frac{3\sqrt{3}π}{7}$ | C. | $\frac{3\sqrt{2}π}{8}$ | D. | $\frac{3\sqrt{2}π}{7}$ |
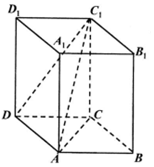 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.