题目内容
11.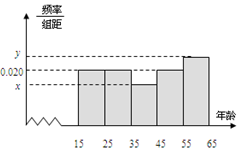 某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了n人,得到如下的统计表和频率分布直方图.(Ⅰ)写出其中的a、b及x和y的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,求这2人中没有第3组人的概率.
| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15,25) | a | 0.10 |
| 第2组 | [25,35) | b | 0.20 |
| 第3组 | [35,45) | 6 | 0.20 |
| 第4组 | [45,55) | 12 | 0.60 |
| 第5组 | [55,65] | 20 | 0.40 |
分析 (Ⅰ)直接利用频率分布直方图,结合累积频率为1,频数=频率×样本容量,可分别求出a,b,x,y的值;
(Ⅱ)直接利用抽样比即可求第1,2,3组每组各抽取人数.
(Ⅲ)列出(Ⅱ)抽取的6人中随机抽取2人是所有情况,求出这2人中没有第3组人的数目,即可求解概率.
解答 解:(Ⅰ)∵第4组人数为$\frac{12}{0.60}$=20人
∴n=$\frac{20}{0.020×10}$=100人(1分)
∴a=0.020×10×100×0.10=2,
b=0.020×10×100×0.20=4,
x=$\frac{\frac{\frac{6}{0.20}}{200}}{10}$=0.015,
y=$\frac{\frac{\frac{20}{0.40}}{200}}{10}$=0.025(5分)
(Ⅱ)第1组应抽$\frac{6}{2+4+6}$×2=1人
第2组应抽$\frac{6}{2+4+6}$×4=2人
第3组应抽$\frac{6}{2+4+6}$×6=3人(9分)
(Ⅲ)第1组抽取的1人为C,设第2组抽取的2人为A1,A2,第3组抽取的3人为B1,B2,B3,
则从6人中抽取2人的基本事件为
A1A2,A1B1,A1B2,A1B3,A1C,A2B1,
A2B2,A2B3,A2C,B1B2,B1B3,B1C,
B2B3,B2C,B3C,共15种,
其中这2人中没有第3组人的有3种,
所以其概率为P=$\frac{3}{15}$=$\frac{1}{5}$ (13分)
点评 本题考查频率分布直方图的应用,分层抽样以及古典概型的概率的求法,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设x>0,y>0,若不等式2log${\;}_{\frac{1}{2}}$[(a-1)x+ay]≤1+log${\;}_{\frac{1}{2}}$(xy)恒成立,则4a的最小值为( )
| A. | $\frac{\sqrt{6}+2}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
16.已知$|\overrightarrow a|=1,|\overrightarrow b|=2$且$<\vec a,\vec b>=120°$则$|2\overrightarrow a+\overrightarrow b|$等于( )
| A. | 4 | B. | 12 | C. | 2 | D. | 2$\sqrt{3}$ |
3.已知双曲线3y2-mx2=3m(m>0)的一个焦点与抛物线y=$\frac{1}{8}$x2的焦点重合,则此双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
1.已知i为虚数单位,则复数$z=\frac{1}{1-i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
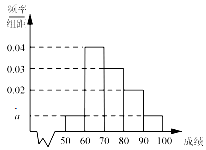 某校100名学生期中考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期中考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].