题目内容
19．平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为90°，$\overrightarrow a=（{2，0}），|{\overrightarrow b}|=1$则$|{\overrightarrow a+2\overrightarrow b}|$=2$\sqrt{2}$．分析 由已知可得$\overrightarrow a$•$\overrightarrow b$=0，结合$\overrightarrow a=（{2，0}），|{\overrightarrow b}|=1$，利用平方法，可得答案．
解答 解：∵平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为90°，
∴$\overrightarrow a$•$\overrightarrow b$=0，
又∵$\overrightarrow a=（{2，0}），|{\overrightarrow b}|=1$，
∴$|{\overrightarrow a+2\overrightarrow b}|$2=${{\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4\overrightarrow{b}}^{2}$=4+4=8，
∴$|{\overrightarrow a+2\overrightarrow b}|$=2$\sqrt{2}$，
故答案为：2$\sqrt{2}$
点评 本题考查的知识点是向量的数量积运算，向量的模，难度中档．
练习册系列答案
相关题目
10．已知x，y都是实数，命题p：|x|＜1；命题q：x2-2x-3＜0，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
7．
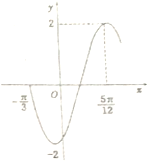函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位后的解析式为（ ）
函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位后的解析式为（ ）| A． | y=2sin（2x-$\frac{π}{6}$） | B． | y=2sin（2x+$\frac{π}{6}$） | C． | y=2sin（2x） | D． | y=2sin（2x+$\frac{π}{3}$） |
11．
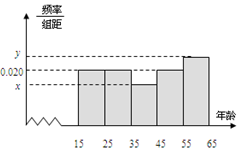某市文化部门为了了解本市市民对当地地方戏曲是否喜爱，从15-65岁的人群中随机抽样了n人，得到如下的统计表和频率分布直方图．
（Ⅰ）写出其中的a、b及x和y的值；
（Ⅱ）若从第1，2，3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人，求这三组每组分别抽取多少人？
（Ⅲ）在（Ⅱ）抽取的6人中随机抽取2人，求这2人中没有第3组人的概率．
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱，从15-65岁的人群中随机抽样了n人，得到如下的统计表和频率分布直方图．（Ⅰ）写出其中的a、b及x和y的值；
（Ⅱ）若从第1，2，3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人，求这三组每组分别抽取多少人？
（Ⅲ）在（Ⅱ）抽取的6人中随机抽取2人，求这2人中没有第3组人的概率．
| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15，25） | a | 0.10 |
| 第2组 | [25，35） | b | 0.20 |
| 第3组 | [35，45） | 6 | 0.20 |
| 第4组 | [45，55） | 12 | 0.60 |
| 第5组 | [55，65] | 20 | 0.40 |
9．已知函数f（x）=sin（πx+$\frac{π}{4}$）和函数g（x）=cos（πx+$\frac{π}{4}$）在区间[-$\frac{5}{4}$，$\frac{7}{4}$]上的图象交于A，B，C三点，则△ABC的面积是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{3\sqrt{2}}{4}$ | C． | $\sqrt{2}$ | D． | $\frac{5\sqrt{2}}{4}$ |