题目内容
16．已知$|\overrightarrow a|=1，|\overrightarrow b|=2$且$＜\vec a，\vec b＞=120°$则$|2\overrightarrow a+\overrightarrow b|$等于（ ）| A． | 4 | B． | 12 | C． | 2 | D． | 2$\sqrt{3}$ |
分析 根据向量的数量积公式计算即可．
解答 解：∵$|\overrightarrow a|=1，|\overrightarrow b|=2$且$＜\vec a，\vec b＞=120°$，
∴$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=1×2×（-$\frac{1}{2}$）=-1，
∴$|2\overrightarrow a+\overrightarrow b|$2=4|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+4$\overrightarrow{a}•\overrightarrow{b}$=4×1+4-4=4，
∴$|2\overrightarrow a+\overrightarrow b|$=2，
故选：C
点评 本题考查了向量的数量积的运算和向量模的计算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
7．
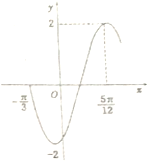函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位后的解析式为（ ）
函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，将f（x）的图象向左平移$\frac{π}{6}$个单位后的解析式为（ ）| A． | y=2sin（2x-$\frac{π}{6}$） | B． | y=2sin（2x+$\frac{π}{6}$） | C． | y=2sin（2x） | D． | y=2sin（2x+$\frac{π}{3}$） |
11．
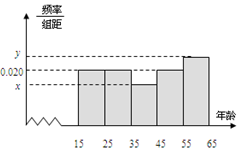某市文化部门为了了解本市市民对当地地方戏曲是否喜爱，从15-65岁的人群中随机抽样了n人，得到如下的统计表和频率分布直方图．
（Ⅰ）写出其中的a、b及x和y的值；
（Ⅱ）若从第1，2，3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人，求这三组每组分别抽取多少人？
（Ⅲ）在（Ⅱ）抽取的6人中随机抽取2人，求这2人中没有第3组人的概率．
某市文化部门为了了解本市市民对当地地方戏曲是否喜爱，从15-65岁的人群中随机抽样了n人，得到如下的统计表和频率分布直方图．（Ⅰ）写出其中的a、b及x和y的值；
（Ⅱ）若从第1，2，3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人，求这三组每组分别抽取多少人？
（Ⅲ）在（Ⅱ）抽取的6人中随机抽取2人，求这2人中没有第3组人的概率．
| 组号 | 分组 | 喜爱人数 | 喜爱人数 占本组的频率 |
| 第1组 | [15，25） | a | 0.10 |
| 第2组 | [25，35） | b | 0.20 |
| 第3组 | [35，45） | 6 | 0.20 |
| 第4组 | [45，55） | 12 | 0.60 |
| 第5组 | [55，65] | 20 | 0.40 |