题目内容
1. 设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD,PA=AB,E为PD中点.
设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD,PA=AB,E为PD中点.(1)求证:直线PD⊥平面AEB;
(2)若直线PC交平面AEB于点F,求直线BF与平面PCD所成的角的正弦值.
分析 (1)证明PD⊥AE,PD⊥AB,推出直线PD⊥平面AEB.
(2)以A为坐标原点,建立如图所示的空间直角坐标系,求出相关点的坐标,平面PCD的法向量,设直线BF与平面PCD所成的角为θ,利用空间向量的数量积求解,直线BF与平面PCD所成的角的正弦值.
解答 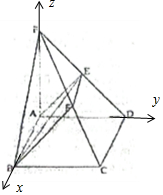 (1)证明:∵PA=AB=AD,E为PD中点,
(1)证明:∵PA=AB=AD,E为PD中点,
∴PD⊥AE,又PA⊥平面ABCD,底面ABCD是正方形,
∴AB⊥面PAD,则PD⊥AB,且AB∩AE=A,∴直线PD⊥平面AEB.
(2)以A为坐标原点,建立如图所示的空间直角坐标系,
∵CD⊥面PAD,∴AE⊥CD,且AE⊥PD,则AE⊥平面PCD,即$\overrightarrow{AE}$为平面PCD的法向量,$\overrightarrow{AE}=({0,\frac{1}{2},\frac{1}{2}})$.AB∥CD,AB∥平面PCD,平面AEB∩平面AEFB=EF,
∴EF∥AB∥CD,又E为PD中点,∴F为PC中点,B(1,0,0),$F({\frac{1}{2},\frac{1}{2},\frac{1}{2}})$,$\overrightarrow{FB}=({\frac{1}{2},-\frac{1}{2},-\frac{1}{2}})$,
设直线BF与平面PCD所成的角为θ,$sinθ=|{cos<\overrightarrow{AE},\overrightarrow{FB}>}|=|{\frac{{-\frac{1}{2}×\frac{1}{2}-\frac{1}{2}×\frac{1}{2}}}{{\sqrt{{{({\frac{1}{2}})}^2}+{{({\frac{1}{2}})}^2}}\sqrt{{{({\frac{1}{2}})}^2}+{{({-\frac{1}{2}})}^2}+{{({-\frac{1}{2}})}^2}}}}}|=\frac{{\sqrt{6}}}{3}$,
则直线BF与平面PCD所成的角的正弦值为$\frac{{\sqrt{6}}}{3}$.
点评 本题考查直线与平面垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力,逻辑推理能力.

| A. | $\sqrt{65}$ | B. | 5$\sqrt{3}$ | C. | $\sqrt{85}$ | D. | $\sqrt{95}$ |
| A. | 2x+3y-12=0 | B. | 2x+3y+12=0 | C. | 2x-3y+12=0 | D. | 2x-3y-12=0 |
| A. | ($\frac{1}{e}$,2)∪(2,e) | B. | ($\frac{1}{e}$+1,e) | C. | (e-1,e) | D. | ($\frac{1}{e}$,e) |