题目内容
6.直线ax+y+3a-1=0恒过定点M,则直线2x+3y-6=0关于M点对称的直线方程为( )| A. | 2x+3y-12=0 | B. | 2x+3y+12=0 | C. | 2x-3y+12=0 | D. | 2x-3y-12=0 |
分析 由直线ax+y+3a-1=0可得定点坐标,设直线2x+3y-6=0关于M点对称的直线方程为2x+3y+c=0,则$\frac{|-6+3-6|}{\sqrt{4+9}}=\frac{|-6+3+c|}{\sqrt{4+9}}$,求出c,即可得出结论.
解答 解:由直线ax+y+3a-1=0,可得a(x+3)+(y-1)=0
令$\left\{\begin{array}{l}{x+3=0}\\{y-1=0}\end{array}\right.$,可得x=-3,y=1,
∴M(-3,1),
设直线2x+3y-6=0关于M点对称的直线方程为2x+3y+c=0,则$\frac{|-6+3-6|}{\sqrt{4+9}}=\frac{|-6+3+c|}{\sqrt{4+9}}$,
∴c=12或c=-6(舍去)
故选B.
点评 本题考查直线恒过定点,考查对称性的运用,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
16.若函数f(x)=sin(x+φ)在x=$\frac{π}{4}$时取得最小值,则函数y=f($\frac{3π}{4}$-x)的一个单调递增区间是( )
| A. | (-$\frac{π}{2}$,-$\frac{π}{4}$) | B. | (0,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{3π}{2}$,2π) |
11.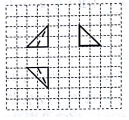 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )| A. | 2+2$\sqrt{3}$+$\sqrt{6}$ | B. | 4+2$\sqrt{3}$+$\sqrt{6}$ | C. | 4+4$\sqrt{3}$+$\sqrt{6}$ | D. | 2+$\sqrt{3}$+$\sqrt{6}$ |
15.函数f(x)=x3-3x2+1的单调递减区间是( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,0) | D. | (0,2) |
16.假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表则当m取下面何值时,X与Y的关系最弱?( )
| y1 | y2 | |
| x1 | 10 | 18 |
| x2 | m | 26 |
| A. | 8 | B. | 9 | C. | 14 | D. | 19 |
 设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD,PA=AB,E为PD中点.
设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD,PA=AB,E为PD中点.