题目内容
13.已知f(x)=$\frac{x}{|lnx|}$,若关于x的方程[f(x)]2-(2m+1)f(x)+m2+m=0恰好有4个不相等的实数根,则实数m的取值范围为( )| A. | ($\frac{1}{e}$,2)∪(2,e) | B. | ($\frac{1}{e}$+1,e) | C. | (e-1,e) | D. | ($\frac{1}{e}$,e) |
分析 求函数的导数,判断函数的取值情况,设t=f(x),利用换元法,将方程转化为一元二次方程,利用根的分布建立条件关系即可得到结论.
解答 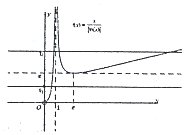 解:令t=f(x),则方程有两个根t1=m或t2=m+1,
解:令t=f(x),则方程有两个根t1=m或t2=m+1,
当x≥0时,f′(x)=$\frac{lnx-1}{l{n}^{2}x}$,
当0≤x<e时,f′(x)<0,当x≥e时,f′(x)≥0
∴f(x)在(0,e)上单调递减,在(e,+∞)单调递增;
作出函数f(x)的草图如图:关于x的方程[f(x)]2-(2m+1)f(x)+m2+m=0恰好有4个不相等的实数根,
转化为t1=f(x)有一个,t2=f(x)有3个,则0<m<e且m+1>e,∴e-1<m<e.
故选C.
点评 本题考查了根的存在性及根的个数的判断,考查了利用函数的导函数分析函数的单调性,考查了学生分析问题和解决问题的能力,利用换元法转化为一元二次方程,是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.设如果执行下面的程序框图,那么输出的S=( )


| A. | 6 | B. | 120 | C. | 12 | D. | 24 |
4.若a=ln2,$b={5^{-\frac{1}{2}}}$,$c=\int_0^{\frac{π}{2}}{\frac{1}{2}cosxdx}$的大小关系为( )
| A. | b<c<a | B. | b<a<c | C. | a<b<c | D. | c<b<a |
3.计算下面事件A与事件B的2×2列联表的χ 2统计量值,得χ 2≈1.779,从而得出结论没有足够的把握认为事件A与事件B相关.
| B | $\overline{B}$ | 总计 | |
| A | 39 | 157 | 196 |
| $\overline{A}$ | 29 | 167 | 196 |
| 总计 | 68 | 324 | 392 |
 设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD,PA=AB,E为PD中点.
设四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD,PA=AB,E为PD中点.