题目内容
8. 已知焦距为2的椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为$\frac{1}{4}$.
已知焦距为2的椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为$\frac{1}{4}$.(1)求椭圆W的标准方程;
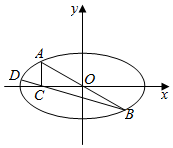
(2)如图所示,点A,D是椭圆W上两点,点A与点B关于原点对称,AD⊥AB,点C在x轴上,且AC与x轴垂直,求证:B,C,D三点共线.
分析 (1)由c=1,a2-b2=1,求得四条直线的斜率,由斜率乘积为$\frac{1}{4}$,代入求得a和b的关系,即可求得a和b的值,求得椭圆W的标准方程;
(2)设A,D的坐标,代入椭圆方程,作差法,求得直线AD的斜率,由kAD•kAB=-1,代入求得$\frac{{y}_{1}}{{x}_{1}}$=$\frac{2({y}_{1}+{y}_{2})}{{x}_{1}+{x}_{2}}$,由kBD-kBC=0,即可求证kBD=kBC,即可求证B,C,D三点共线.
解答 解:(1)由题意可知:2c=2,c=1,a2-b2=1,
∵M(x0,y0)为椭圆W上不在坐标轴上的任意一点,
∴$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,${y}_{0}^{2}$=$\frac{{b}^{2}}{{a}^{2}}$(a2-${x}_{0}^{2}$),${x}_{0}^{2}$=$\frac{{a}^{2}}{{b}^{2}}$(b2-${y}_{0}^{2}$),
${k}_{M{A}_{1}}$•${k}_{M{A}_{2}}$•${k}_{{MB}_{1}}$•${k}_{M{B}_{2}}$=$\frac{{y}_{0}}{{x}_{0}+a}$•$\frac{{y}_{0}}{{x}_{0}-a}$•$\frac{{y}_{0}-b}{{x}_{0}}$•$\frac{{y}_{0}+b}{{x}_{0}}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-{a}^{2}}$•$\frac{{y}_{0}^{2}-{b}^{2}}{{x}_{0}^{2}}$,
=$\frac{\frac{{b}^{2}}{{a}^{2}}({a}^{2}-{x}_{0}^{2})}{{x}_{0}^{2}-{a}^{2}}$•$\frac{{y}_{0}^{2}-{b}^{2}}{\frac{{a}^{2}}{{b}^{2}}({b}^{2}-{y}_{0}^{2})}$=($\frac{{b}^{2}}{{a}^{2}}$)2=$\frac{1}{4}$,则a2=2b2,
∴a2=2,b2=1,
∴椭圆W的标准方程$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)证明:不妨设点A(x1,y1),D(x2,y2),B的坐标(-x1,-y1),C(x1,0),
∵A,D在椭圆上,$\left\{\begin{array}{l}{{x}_{1}^{2}+2{y}_{1}^{2}=1}\\{{x}_{2}^{2}+2{y}_{2}^{2}=1}\end{array}\right.$,=0,即(x1-x2)(x1+x2)+2(y1-y2)(y1+y2)=0,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{2({y}_{1}+{y}_{2})}$,
由AD⊥AB,
∴kAD•kAB=-1,$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-1,$\frac{{y}_{1}}{{x}_{1}}$•(-$\frac{{x}_{1}+{x}_{2}}{2({y}_{1}+{y}_{2})}$,)=-1,
∴$\frac{{y}_{1}}{{x}_{1}}$=$\frac{2({y}_{1}+{y}_{2})}{{x}_{1}+{x}_{2}}$,
∴kBD-kBC=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$-$\frac{{y}_{1}}{2{x}_{1}}$=$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$-$\frac{{y}_{1}+{y}_{2}}{{x}_{1}+{x}_{2}}$=0,
kBD=kBC,
∴B,C,D三点共线.
点评 本题考查椭圆的简单几何性质,直线的斜率公式,考查计算能力,考查分析问题及解决问题的能力,属于中档题.

| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 0 |
| 温度t(℃) | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
| 生长速度y | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
(2)利用(1)中的线性回归方程,分析气温从-50C至200C时生长速度的变化情况,如果某月的平均气温是20C时,预测这月大约能生长多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline{xy}}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}},\hat a=\overline y-\hat b\overline x$.
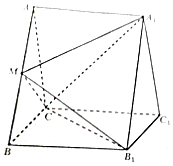 如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=CC1=2,M是AB的中点.
如图,三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠ACB=90°,AC=CB=CC1=2,M是AB的中点.(1)求证:平面A1CM⊥平面ABB1A1;
(2)求点M到平面A1CB1的距离.
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
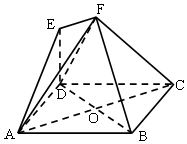 如图,多面体EF-ABCD中,ABCD是正方形,AC、BD相交于O,EF∥AC,点E在AC上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,ABCD是正方形,AC、BD相交于O,EF∥AC,点E在AC上的射影恰好是线段AO的中点.