题目内容
3.已成椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右顶点分别为A1、A2,上下顶点分别为B2/B1,左右焦点分别为F1、F2,其中长轴长为4,且圆O:x2+y2=$\frac{12}{7}$为菱形A1B1A2B2的内切圆.(1)求椭圆C的方程;
(2)点N(n,0)为x轴正半轴上一点,过点N作椭圆C的切线l,记右焦点F2在l上的射影为H,若△F1HN的面积不小于$\frac{3}{16}$n2,求n的取值范围.
分析 (1)由题意求得a,直线A2B2的方程为$\frac{x}{2}+\frac{y}{b}=1$,利用点到直线的距离公式,即可求得b的值,求得椭圆C的方程;
(2)设直线方程,代入椭圆方程,由△=0,求得m和n的关系,利用三角形的面积公式,求得m的取值范围,代入即可求得n的取值范围.
解答 解:(1)由题意知2a=4,所以a=2,
所以A1(-2,0),A2(2,0),B1(0,-b),B2(0,b),则
直线A2B2的方程为$\frac{x}{2}+\frac{y}{b}=1$,即bx+2y-2b=0,
所以$\frac{丨-2b丨}{\sqrt{4+{b}^{2}}}$=$\sqrt{\frac{12}{7}}$,解得b2=3,
故椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由题意,可设直线l的方程为x=my+n,m≠0,
联立$\left\{\begin{array}{l}{x=my+n}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,消去x得(3m2+4)y2+6mny+3(n2-4)=0,(*)
由直线l与椭圆C相切,得△=(6mn)2-4×3×(3m2+4)(n2-4)=0,
化简得3m2-n2+4=0,
设点H(mt+n,t),由(1)知F1(-1,0),F2(1,0),则$\frac{t-0}{(mt+n)-1}$•$\frac{1}{m}$=-1,
解得:t=-$\frac{m(n-1)}{1+{m}^{2}}$,
所以△F1HN的面积${S}_{△{F}_{1}HN}$=$\frac{1}{2}$(n+1)丨-$\frac{m(n-1)}{1+{m}^{2}}$丨=$\frac{1}{2}$$\frac{丨m({n}^{2}-1)丨}{1+{m}^{2}}$,
代入3m2-n2+4=0,消去n化简得${S}_{△{F}_{1}HN}$=$\frac{3}{2}$丨m丨,
所以$\frac{3}{2}$丨m丨≥$\frac{3}{16}$n2=$\frac{3}{16}$(3m2+4),解得$\frac{2}{3}$≤丨m丨≤2,即$\frac{4}{9}$≤m2≤4,
从而$\frac{4}{9}$≤$\frac{{n}^{2}-4}{3}$≤4,又n>0,
所以$\frac{4\sqrt{3}}{3}$≤n≤4,
故n的取值范围为[$\frac{4\sqrt{3}}{3}$,4].
点评 本题考查椭圆的标准方程及简单几何性质,考查韦达定理,三角形的面积公式,考查计算能力,属于中档题.


| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
| A. | -$\frac{5}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{21}{2}$ | D. | $\frac{21}{2}$ |
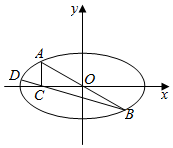 已知焦距为2的椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为$\frac{1}{4}$.
已知焦距为2的椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为A1,A2,上、下顶点分别为B1,B2,点M(x0,y0)为椭圆W上不在坐标轴上的任意一点,且四条直线MA1,MA2,MB1,MB2的斜率之积为$\frac{1}{4}$.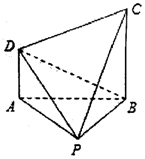 如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.
如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2. 如图,四棱锥P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD 都是边长为2的等边三角形,E 是BC的中点.
如图,四棱锥P-ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD 都是边长为2的等边三角形,E 是BC的中点.