题目内容
18．若点P（a，b）是直线$y=\sqrt{3}x-\sqrt{3}$上的点，则（a+1）2+b2的最小值是（ ）| A． | 3 | B． | $\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 0 |
分析 求出M（-1，0）到直线的距离d，即可得出（a+1）2+b2的最小值=d2．
解答 解：求出M（-1，0）到直线的距离d=$\frac{|-\sqrt{3}-\sqrt{3}|}{2}$=$\sqrt{3}$，
∴（a+1）2+b2的最小值=d2=3．
故选：A．
点评 本题考查了点到直线的距离公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（x个周）和市场占有率（y%）的几组相关数据如表：
（Ⅰ）根据表中的数据，用最小二乘法求出y关于x的线性回归方程$\widehat{y}=\widehat{b}x+\widehat{a}$；
（Ⅱ）根据上述线性回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个周，该款旗舰机型市场占有率能超过0.40%（最后结果精确到整数）．
参考公式：$\widehat{b}=\frac{{{\sum_{i=1}^{n}x}_{i}y}_{y}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$，$\hat a=\bar y-\hat b\bar x$．
| x | 1 | 2 | 3 | 4 | 5 |
| y | 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
（Ⅱ）根据上述线性回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个周，该款旗舰机型市场占有率能超过0.40%（最后结果精确到整数）．
参考公式：$\widehat{b}=\frac{{{\sum_{i=1}^{n}x}_{i}y}_{y}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$，$\hat a=\bar y-\hat b\bar x$．
10．下列角中，与$-\frac{5π}{6}$终边相同的角是（ ）
| A． | $-\frac{11π}{6}$ | B． | $\frac{11π}{6}$ | C． | $-\frac{7π}{6}$ | D． | $\frac{7π}{6}$ |
7．已知tanα=2，则$\frac{2sinα+cosα}{sinα-cosα}$的值为（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
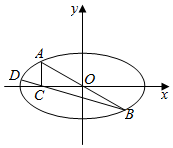已知焦距为2的椭圆W：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为A1，A2，上、下顶点分别为B1，B2，点M（x0，y0）为椭圆W上不在坐标轴上的任意一点，且四条直线MA1，MA2，MB1，MB2的斜率之积为$\frac{1}{4}$．