题目内容
3.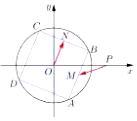 如图,正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点,已知点P(2,0),当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围是( )
如图,正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点,已知点P(2,0),当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围是( )| A. | [-1,1] | B. | $[{-\sqrt{2},\sqrt{2}}]$ | C. | [-2,2] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
分析 由平面几何知识可得OM=ON,设M(cosα,sinα),用α表示出$\overrightarrow{PM}$和$\overrightarrow{ON}$,得到$\overrightarrow{PM}•\overrightarrow{ON}$关于α的函数,根据三角函数的性质得出答案.
解答 解:圆O的半径r=$\sqrt{2}$,∴正方形的边长为1,
∴OM=ON=1,设M(cosα,sinα),则N(cos($\frac{π}{2}+α$),sin($\frac{π}{2}+α$)),即N(-sinα,cosα),
∴$\overrightarrow{PM}$=(cosα-2,sinα),$\overrightarrow{ON}$=(-sinα,cosα),
∴$\overrightarrow{PM}•\overrightarrow{ON}$=2sinα-sinαcosα+sinαcosα=2sinα,
∵-1≤sinα≤1,∴-2≤2sinα≤2,
故选:C.
点评 本题考查了平面向量的数量积运算,三角函数的性质,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
18.已知离散型随机变量X的分布列为
则变量X的数学期望E(X)=1,方差D(X)=$\frac{1}{2}$.
| X | 0 | 1 | 2 |
| P | a | $\frac{1}{2}$ | $\frac{1}{4}$ |
19.已知m,n是空间两条不同的直线,α,β是空间两个不同的平面,下列命题为真命题的是( )
| A. | 若m∥α,m∥β,则α∥β | B. | 若α∥β,m?α,n⊥β,则m⊥n | ||
| C. | 若m⊥α,m⊥n,则n∥α | D. | 若α⊥β,m?α,n⊥β,则m∥n |
18.不等式|x|•(1-2x)>0的解集是( )
| A. | $(-∞,\frac{1}{2})$ | B. | (-∞,0)∪$(0,\frac{1}{2})$ | C. | $(\frac{1}{2},+∞)$ | D. | $(0,\frac{1}{2})$ |
8.下列结论:①(sin x)′=-cos x;②($\frac{1}{x}$)′=$\frac{1}{{x}^{2}}$;③(log3x)′=$\frac{1}{3lnx}$;④(ln x)′=$\frac{1}{x}$.其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |