题目内容
15.已知O是△ABC所在平面内一点,向量$\overrightarrow{O{P_1}}、\overrightarrow{O{P_2}}、\overrightarrow{O{P_3}}$满足条件$\overrightarrow{O{P_1}}+\overrightarrow{O{P_2}}+\overrightarrow{O{P_3}}$=$\overrightarrow 0$,且$|{\overrightarrow{O{P_1}}}|=|{\overrightarrow{O{P_2}}}|=|{\overrightarrow{O{P_3}}}$|=1,则△P1P2P3是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
分析 根据向量的运算法则计算出|$\overrightarrow{{P}_{1}{P}_{2}}$|=|$\overrightarrow{{P}_{1}{P}_{3}}$|=|$\overrightarrow{{P}_{2}{P}_{3}}$|=$\sqrt{3}$,从而判断三角形的形状.
解答 解:∵$\overrightarrow{O{P_1}}+\overrightarrow{O{P_2}}+\overrightarrow{O{P_3}}=\overrightarrow 0$,
∴$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$=-$\overrightarrow{O{P}_{3}}$,
∴($\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$)2=(-$\overrightarrow{O{P}_{3}}$)2,
∴${\overrightarrow{O{P}_{1}}}^{2}$+2$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$+${\overrightarrow{O{P}_{2}}}^{2}$=${\overrightarrow{O{P}_{3}}}^{2}$,
∵$|{\overrightarrow{O{P_1}}}|=|{\overrightarrow{O{P_2}}}|=|{\overrightarrow{O{P_3}}}|=1$,
∴|$\overrightarrow{O{P}_{1}}$|2+|$\overrightarrow{O{P}_{2}}$|2=|$\overrightarrow{O{P}_{3}}$|2=1,
∴$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$=-$\frac{1}{2}$,
∴|$\overrightarrow{{P}_{1}{P}_{2}}$|2=|$\overrightarrow{O{P}_{2}}$-$\overrightarrow{O{P}_{1}}$|2=${\overrightarrow{O{P}_{2}}}^{2}$-$\overrightarrow{O{P}_{1}}$•$\overrightarrow{O{P}_{2}}$+${\overrightarrow{O{P}_{1}}}^{2}$=3,
∴|$\overrightarrow{{P}_{1}{P}_{2}}$|=$\sqrt{3}$,
同理|$\overrightarrow{{P}_{1}{P}_{3}}$|=|$\overrightarrow{{P}_{2}{P}_{3}}$|=$\sqrt{3}$,
∴△P1P2P3是等边三角形,
故选:D
点评 本题考查了向量的运算,向量垂直问题,是一道中档题.

| A. | $4±\sqrt{15}$ | B. | $±\frac{1}{3}$ | C. | 1或7 | D. | $1±\sqrt{6}$ |
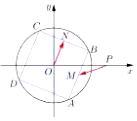 如图,正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点,已知点P(2,0),当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围是( )
如图,正方形ABCD内接于圆O:x2+y2=2,M,N分别为边AB,BC的中点,已知点P(2,0),当正方形ABCD绕圆心O旋转时,$\overrightarrow{PM}•\overrightarrow{ON}$的取值范围是( )| A. | [-1,1] | B. | $[{-\sqrt{2},\sqrt{2}}]$ | C. | [-2,2] | D. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ |
| A. | {x|2≤x<6} | B. | {x|0≤x<6} | C. | {0,1,2,3,4,5} | D. | {2,3,4,5} |