题目内容
(1)已知全集U=A∪B={x∈N|0≤x≤10},A∩(∁UB)={1,3,5,7},试求集合B.
(2)已知lg2=a,lg3=b,试用a,b表示log125.
(2)已知lg2=a,lg3=b,试用a,b表示log125.
考点:对数的运算性质,交、并、补集的混合运算
专题:函数的性质及应用
分析:(1)由于全集U=A∪B={x∈N|0≤x≤10}={0,1,2,3,4,5,6,7,8,9,10},A∩(∁UB)={1,3,5,7},可得1,3,5,7∈∁UB.即可得出B.
(2)由lg2=a,lg3=b,可得log125=
=
,即可得出.
(2)由lg2=a,lg3=b,可得log125=
| lg5 |
| 2lg2+lg3 |
| 1-lg2 |
| 2lg2+lg3 |
解答:
解:(1)∵全集U=A∪B={x∈N|0≤x≤10}={0,1,2,3,4,5,6,7,8,9,10},A∩(∁UB)={1,3,5,7},
∴1,3,5,7∈∁UB.
∴B={0,2,4,6,8,10}.
(2)∵lg2=a,lg3=b,
∴log125=
=
=
.
∴1,3,5,7∈∁UB.
∴B={0,2,4,6,8,10}.
(2)∵lg2=a,lg3=b,
∴log125=
| lg5 |
| 2lg2+lg3 |
| 1-lg2 |
| 2lg2+lg3 |
| 1-a |
| 2a+b |
点评:本题考查了集合的运算、对数的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
为了得到函数f(x)=2sin(2x-
)的图象,只要将y=2sinx的图象上所有的点( )
| π |
| 3 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
在空间直角坐标系中,A1是点A(-3,4,0)关于B(-1,2,3)的对称点,则|AA1|=( )
A、2
| ||
B、2
| ||
| C、9 | ||
D、2
|
已知集合A={z||z|≤2,z∈C},集合B={z|z=1+ai,a∈R},其中C为复数集,i为虚数单位,若A∩B≠∅,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、(-
| ||||
C、(-∞,-
| ||||
D、[-
|
设全集为实数集R,M={x|x2>4},N={x|1<x≤3},则图中阴影部分表示的集合是( ) 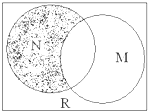

| A、{x|1-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |
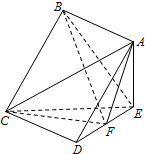 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.