题目内容
数列{an}中,a1=1,Sn为数列{an}前n项和an=
(n≥2),求Sn和an.
| ||
| 2Sn-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:由an=
(n≥2),得sn-sn-1=
(n≥2),整理得,
-
=-1,又
=
=1,故数列{
}是首项为1,公差为-1的等差数列,即可求得结论.
| ||
| 2Sn-1 |
| ||
| 2Sn-1 |
| 1 |
| sn |
| 1 |
| sn-1 |
| 1 |
| s1 |
| 1 |
| a1 |
| 1 |
| sn |
解答:
解:由an=
(n≥2),得
sn-sn-1=
(n≥2),
整理得,sn-sn-1=snsn-1,
∴
-
=-1,
又
=
=1,
∴数列{
}是首项为1,公差为-1的等差数列,
∴
=1-(n-1)=2-n,
∴sn=
.
an=
=
.
| ||
| 2Sn-1 |
sn-sn-1=
| ||
| 2Sn-1 |
整理得,sn-sn-1=snsn-1,
∴
| 1 |
| sn |
| 1 |
| sn-1 |
又
| 1 |
| s1 |
| 1 |
| a1 |
∴数列{
| 1 |
| sn |
∴
| 1 |
| sn |
∴sn=
| 1 |
| 2-n |
an=
| ||
| 2Sn-1 |
| 2 |
| 2n-n2 |
点评:本题考查利用公式法求数列的通项公式,解题时注意式子的合理变形,属于基础题.

练习册系列答案
相关题目
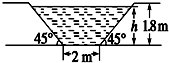 如图,某灌溉渠的横断面是等腰梯形,底宽为2m,渠深为1.8m,斜坡的倾斜角是45°.(临界状态不考虑)
如图,某灌溉渠的横断面是等腰梯形,底宽为2m,渠深为1.8m,斜坡的倾斜角是45°.(临界状态不考虑)