题目内容
3.已知O为△ABC内一点,且$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$,$\overrightarrow{AD}=t\overrightarrow{AC}$,若B,O,D三点共线,则t的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 以OB,OC为邻边作平行四边形OBFC,连接OF与 BC相交于点E,E为BC的中点.由$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$,可得$\overrightarrow{OB}+\overrightarrow{OC}$=2$\overrightarrow{AO}$=2$\overrightarrow{OE}$,点O是直线AE的中点.根据$\overrightarrow{AD}=t\overrightarrow{AC}$,B,O,D三点共线,可得点D是BO与AC的交点.过点O作OM∥BC交AC于点M,则点M为AC的中点.即可得出.
解答 解:以OB,OC为邻边作平行四边形OBFC,连接OF与 BC相交于点E,E为BC的中点.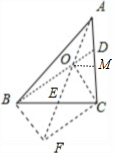
∵$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$,∴$\overrightarrow{OB}+\overrightarrow{OC}$=2$\overrightarrow{AO}$=2$\overrightarrow{OE}$,
∴点O是直线AE的中点.
∵$\overrightarrow{AD}=t\overrightarrow{AC}$,B,O,D三点共线,
∴点D是BO与AC的交点.
过点O作OM∥BC交AC于点M,则点M为AC的中点.
则OM=$\frac{1}{2}$EC=$\frac{1}{4}$BC,$\frac{DM}{DC}$=$\frac{1}{4}$,
∴DM=$\frac{1}{3}$MC,
∴AD=$\frac{2}{3}$AM=$\frac{1}{3}$AC,
∴t=$\frac{1}{3}$.
故选:B.
点评 本题考查了向量共线定理、向量三角形与平行四边形法则、平行线的性质,考查了推理能力与计算能力,属于中档题.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案| A. | {1} | B. | {4} | C. | {1,3} | D. | {1,4} |

| A. | a>0,c<0,d>0 | B. | a>0,c>0,d<0 | C. | a<0,c<0,d<0 | D. | a<0,c>0,d<0 |
| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $2-\sqrt{2}$ |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | 1 |
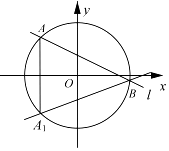 在平面直角坐标系xOy中,已知圆C:x2+y2=4和动直线l:x=my+1.
在平面直角坐标系xOy中,已知圆C:x2+y2=4和动直线l:x=my+1.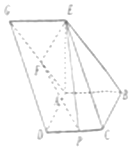 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE=2.