题目内容
13.已知$f(x)=3sin({ωx+\frac{π}{6}})({ω>0})$,若f(x)图象向左平移$\frac{π}{6}$个单位后图象与y=3cosωx图象重合.(1)求ω的最小值;
(2)在条件(1)下将下表数据补充完整,并用“五点法”作出f(x)在一个周期内的图象.
| $ωx+\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | |||||
| f(x) |
分析 (1)把f(x)图象向左平移$\frac{π}{6}$个单位后,得到y=3sin[ω(x+$\frac{π}{6}$)+$\frac{π}{6}$]=3sin(ωx+$\frac{π}{6}$ω+$\frac{π}{6}$)的图象,再根据所得到的图象与函数y=3cosωx的图象重合,即可求ω的最小值;
(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
解答 解:(1)把f(x)图象向左平移$\frac{π}{6}$个单位后,得到y=3sin[ω(x+$\frac{π}{6}$)+$\frac{π}{6}$]=3sin(ωx+$\frac{π}{6}$ω+$\frac{π}{6}$)的图象,
再根据所得到的图象与函数y=3cosωx的图象重合,
可得sin(ωx+$\frac{π}{6}$ω+$\frac{π}{6}$)=cosωx,故$\frac{π}{6}$ω+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,
即ω=12k+2,∵ω>0,∴ω的最小值2;
(2)列表:
| 2x+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 3 | 0 | -3 | 0 |
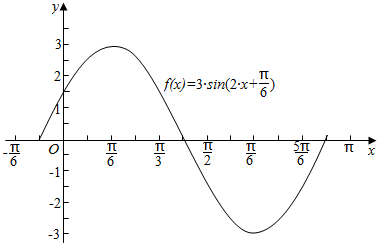 .
.点评 本题主要考查函数y=Asin(ωx+φ)的图象性质,用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,属于基础题.

练习册系列答案
相关题目
19.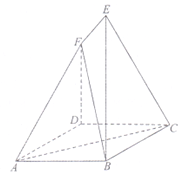 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
(Ⅰ)求证:EF丄AC;
(Ⅱ)求直线CE与平面ABF所成角的正弦值.
 如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a
如图,ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD=$\sqrt{3}$a(Ⅰ)求证:EF丄AC;
(Ⅱ)求直线CE与平面ABF所成角的正弦值.
5.已知f(x)=$\frac{{e}^{x}}{x}$,若方程f2(x)+2a2=3a|f(x)|有且仅有4个不等实根,则实数a的取值范围为( )
| A. | (0,$\frac{e}{2}$) | B. | ($\frac{e}{2}$,e) | C. | (0,e) | D. | (e,+∞) |
2.集合A={-2,-1,0,1,2},B={-1,2,3},则A∪B=( )
| A. | {-2,-1,0,1,2} | B. | {-1,2,3} | C. | {-2,-1,0,1,2,3} | D. | {-1,2} |
3.已知等差数列{an}中,a1=11,a5=-1,则{an}的前n项和Sn的最大值是( )
| A. | 15 | B. | 20 | C. | 26 | D. | 30 |