题目内容
6.若($\frac{1}{x}$+2x)6展开式的常数项为( )| A. | 120 | B. | 160 | C. | 200 | D. | 240 |
分析 先求出二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项.
解答 解($\frac{1}{x}$+2x)6的展开式的通项公式为Tr+1=C6r2rx2r-6.
令2r-6=0,解得r=3,
∴($\frac{1}{x}$+2x)6展开式的常数项为C6323=160,
故选:B
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
14.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}&{\;}\\{ax+y≥4}&{\;}\\{x-2y+3≥0}&{\;}\end{array}\right.$,目标函数z=2x-3y的最大值是2,则实数a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
1.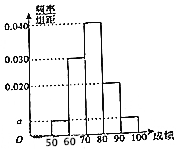 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
(Ⅰ)求图中a的值;
(Ⅱ)估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表);
(Ⅲ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
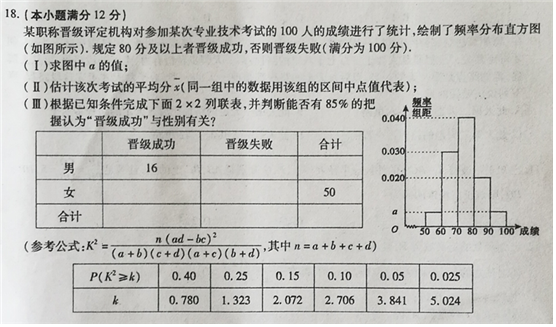
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分).(Ⅰ)求图中a的值;
(Ⅱ)估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表);
(Ⅲ)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
| 晋级成功 | 晋级失败 | 合计 | |
| 男 | 16 | ||
| 女 | 50 | ||
| 合计 |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |

11.已知函数f(x)是定义在R上的可导函数,其导函数为f′(x),则命题P:“?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017”是命题Q:“?x∈R,|f′(x)|<2017”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知抛物线y2=2px(p>0)过点A($\frac{1}{2}$,$\sqrt{2}$),其准线与x轴交于点B,直线AB与抛物线的另一个交点为M,若$\overrightarrow{MB}$=λ$\overrightarrow{AB}$,则实数λ为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |