题目内容
由直线y=
,y=2,曲线y=
及y轴所围成的封闭图形的面积是( )
| 1 |
| 2 |
| 1 |
| x |
| A、2ln2 | ||
| B、2ln2-1 | ||
C、
| ||
D、
|
考点:定积分
专题:导数的综合应用
分析:利用定积分的几何意义,首先利用定积分表示出图形的面积,求出原函数,计算即可.
解答:
解:由题意,直线y=
,y=2,曲线y=
及y轴所围成的封闭图形的面积如图阴影部分,

面积为
dy=lny
=ln2-ln
=2ln2;
故选A.
| 1 |
| 2 |
| 1 |
| x |

面积为
| ∫ | 2
|
| 1 |
| y |
| | | 2
|
| 1 |
| 2 |
故选A.
点评:本题考查定积分的运用,利用定积分的几何意义求曲边梯形的面积,考查了学生的计算能力,属于基础题.

练习册系列答案
相关题目
设O为原点,M(2,-1),若点N(x,y)满足不等式组
,则
•
的最小值是( )
|
| OM |
| ON |
| A、-3 | B、-2 | C、-1 | D、0 |
设p:f(x)=x3-2x2-mx+1在(-∞,+∞)上单调递增;q:m>
,则p是q的( )
| 4 |
| 3 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、以上都不对 |
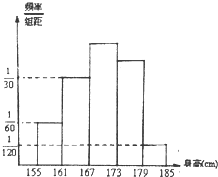 某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )
某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )