题目内容
已知数列{an}的前n项和为Sn,a1=-
,满足Sn+
+2=an(n≥2).
(1)计算S1,S2,S3,S4;
(2)由(1)猜想Sn的表达式.
| 2 |
| 3 |
| 1 |
| Sn |
(1)计算S1,S2,S3,S4;
(2)由(1)猜想Sn的表达式.
考点:归纳推理,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)由题设得Sn-1Sn+2Sn+1=0,代入计算,即可计算S1,S2,S3,S4;
(2)由(1)猜想Sn的表达式.
(2)由(1)猜想Sn的表达式.
解答:
解:(1)由题设得Sn2+2Sn+1-anSn=0,当n≥2(n∈N*)时,an=Sn-Sn-1,
代入上式,得Sn-1Sn+2Sn+1=0.(*)
S1=a1=-
,
令n=2可得S2+
=a2-2=S2-a1-2,∴S2=-
,
同理S3=-
,S4=-
(2)由(1)猜想Sn=-
.
代入上式,得Sn-1Sn+2Sn+1=0.(*)
S1=a1=-
| 2 |
| 3 |
令n=2可得S2+
| 1 |
| S2 |
| 3 |
| 4 |
同理S3=-
| 4 |
| 5 |
| 5 |
| 6 |
(2)由(1)猜想Sn=-
| n+1 |
| n+2 |
点评:本题考查归纳推理,考查数列递推式,考查学生的计算能力,比较基础.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
下列命题正确的是( )
| A、经过三点确定一个平面 |
| B、经过一条直线和一个点确定一个平面 |
| C、两两相交且不共点的三条直线确定一个平面 |
| D、四边形确定一个平面 |
定义在R上的函数f(x),g(x)的导函数分别为f′(x),g′(x)且f′(x)<g′(x).则下列结论一定成立的是( )
| A、f(1)+g(0)<g(1)+f(0) |
| B、f(1)+g(0)>g(1)+f(0) |
| C、f(1)-g(0)>g(1)-f(0) |
| D、f(1)-g(0)<g(1)-f(0) |
设函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x-2x+m(m为常数),则f(-2)等于( )
A、-
| ||
| B、-1 | ||
| C、1 | ||
| D、3 |
圆的方程为x2+y2+kx+2y+k2=0,当圆面积最大时,圆心坐标为( )
| A、(-1,1) |
| B、(1,-1) |
| C、(-1,0) |
| D、(0,-1) |
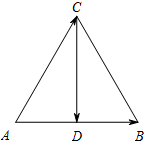 如图,已知正三角形ABC的边长为1,设
如图,已知正三角形ABC的边长为1,设