题目内容
17.直线$y=\frac{π}{4}$与函数f(x)=tanωx(ω>0)图象相交的相邻两点间距离为$\frac{π}{4}$,则$f(\frac{π}{4})$的值是0.分析 先根据函数f(x)=tanωx 的图象结合题意求出其最小正周期,求出ω的值确定函数f(x)的解析式,最后将x=$\frac{π}{4}$代入即可求出答案.
解答 解:类比正切函数的图象知,
f(x)=tanωx被平行于x轴的直线所截得的长度为一个周期长度,
由此可得$T=\frac{π}{4}$,那么ω=4,
则$f(\frac{π}{4})=tanπ=0$,
故答案为:0.
点评 本题主要考查正切函数的性质和最小正周期的求法.考查基础知识的运用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
8.若A(-2,3),B(3,-2),C(1,m)三点共线,则m的值为( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | -2 | D. | 0 |
5.定义在R上的函数f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,函数f(x-1)的图象关于(1,0)成中心对称,如果实数m,n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是( )
| A. | (9,49) | B. | (13,49) | C. | (9,25) | D. | (3,7) |
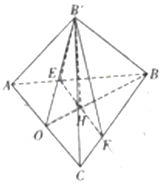 如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.
如图,等腰△ABC中,AB=BC=5,AC=6,点E,F分别在AB,BC上,AE=CF=$\frac{5}{4}$,O为AC边上的中点,EF交BO于点H,将△BEF沿EF折到△B′EF的位置,OB′=$\sqrt{10}$.