题目内容
5.定义在R上的函数f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,函数f(x-1)的图象关于(1,0)成中心对称,如果实数m,n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是( )| A. | (9,49) | B. | (13,49) | C. | (9,25) | D. | (3,7) |
分析 由题意可知函数单调递增,将不等式转化成f(m2-6m+21)<f(n2-8n)=f(-n2+8n),由函数的单调性整理得:(m-3)2+(n-4)2<4,则表示m2+n2表示的是阴影部分的点到原点的距离.
解答 解:函数f(x-1)的图象关于点(1,0)中心对称,则函数y=f(x)关于原点对称,即f(x)为奇函数;,
由f(m2-6m+21)+f(n2-8n)<0得f(m2-6m+21)<f(n2-8n)=f(-n2+8n),
又由在R上f(x)对任意x1,x2(x1≠x2)都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>0$,
∴函数y=f(x)是定义在R上的增函数,
则m2-6m+21<-n2+8n,
∴(m-3)2+(n-4)2<4,表示以以(3,4)为圆心,以2为半径的圆的内部,
∴实数m,n满足不等式f(m2-6m+21)+f(n2-8n)<0,即满足(m-3)2+(n-4)2<4,
作出图象,m2+n2表示圆内部的点到原点的距离的平方,
则圆心到原点的距离d=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴(m-3)2+(n-4)2=4内部的点到原点的距离范围(5-2,5+2),即(3,7),
∴m2+n2的取值范围(9,49),
故选A.
点评 本题考查导数的综合应用,考查函数的单调性,对称性及函数的奇偶性,考查点到直线的距离公式,考查计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.抛物线y=4-x2与直线y=4x的两个交点为A、B,点P在抛物线上从A向B运动,当△PAB的面积为最大时,点P的坐标为( )
| A. | (-3,-5) | B. | (-2,0) | C. | (-1,3) | D. | (0,4) |
13.下列函数为奇函数的是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x-1 | C. | y=x2 | D. | y=x3 |
10.下面表格是两种教学实验的成绩对比统计,试分析两种教法的效果.
| 及格 | 不及格 | 合计 | |
| 掌握教学法 | 36 | 8 | 44 |
| 常规教学法 | 40 | 16 | 56 |
| 合计 | 76 | 24 | 100 |
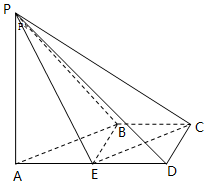 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.