题目内容
8.若A(-2,3),B(3,-2),C(1,m)三点共线,则m的值为( )| A. | $\frac{1}{2}$ | B. | -1 | C. | -2 | D. | 0 |
分析 根据三点共线与斜率的关系即可得出.
解答 解:kAB=$\frac{-2-3}{3-(-2)}$=-1,kAC=$\frac{3-m}{-2-1}$=$-\frac{3-m}{3}$.
∵A(-2,3),B(3,-2),C(1,m)三点共线,
∴-1=$-\frac{3-m}{3}$,解得m=0.
故选:D.
点评 本题考查了三点共线与斜率的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
19.定义在(0,$\frac{π}{2}$),上的函数f(x),f′(x)是导函数,满足f(x)<f′(x)tanx,则下列表达式正确的是( )
| A. | $\sqrt{3}$•f($\frac{π}{4}$)>$\sqrt{2}$•f($\frac{π}{3}$) | B. | f(1)>2•f($\frac{π}{6}$)•sin1 | C. | $\sqrt{2}$•f($\frac{π}{6}$)>f($\frac{π}{4}$) | D. | $\sqrt{3}$•f($\frac{π}{6}$)>f($\frac{π}{3}$) |
3.已知数列{an}满足an=an-1+an-2(n>2,n∈N*),且a2015=1,a2017=-1,设{an}的前n项和为Sn,则S2020-S2016=( )
| A. | -17 | B. | -15 | C. | -6 | D. | 0 |
13.下列函数为奇函数的是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x-1 | C. | y=x2 | D. | y=x3 |
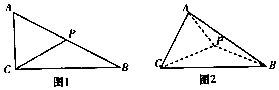 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得$AB=\sqrt{10}$.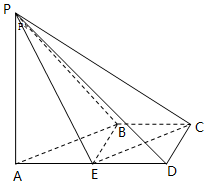 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD=1,E为棱AD的中点,异面直线PA与CD所成的角为90°.