题目内容
14．执行如图所示的程序框图，若输入的x值为2，则输出v的值为（ ）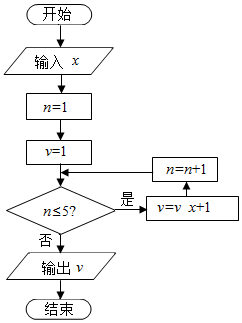
| A． | 31 | B． | 32 | C． | 63 | D． | 64 |
分析 模拟执行程序，依次写出每次循环得到的v，n的值，当n=6时不满足条件n≤5，退出循环，输出v的值为63即可得解．
解答 解：模拟执行程序，可得
x=2，n=1，v=1
满足条件n≤5，执行循环体，v=3，n=2
满足条件n≤5，执行循环体，v=7，n=3
满足条件n≤5，执行循环体，v=15，n=4
满足条件n≤5，执行循环体，v=31，n=5
满足条件n≤5，执行循环体，v=63，n=6
不满足条件n≤5，退出循环，输出v的值为63．
故选：C．
点评 本题考查的知识点是程序框图，在写程序的运行结果时，我们常使用模拟循环的变法，但程序的循环体中变量比较多时，要用列举法对数据进行管理，属于基础题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
4．当1＜m＜$\frac{3}{2}$时，复数（3+i）-m（2+i）在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
2．某空调专卖店试销A、B、C三种新型空调，销售情况如表所示：
（1）求A型空调前三周的平均周销售量；
（2）根据C型空调前三周的销售情况，预估C型空调五周的平均周销售量为10台，当C型空调周销售量的方差最小时，求C4，C5的值；
（注：方差s2=$\frac{1}{n}$[x1-$\overline{x}$）2+（x${\;}_{2}-\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为x1，x2，…，xn的平均数）
（3）为跟踪调查空调的使用情况，根据销售记录，从第二周和第三周售出的空调中分别随机抽取一台，求抽取的两台空调中A型空调台数X的分布列及数学期望．
| 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | |
| A型数量（台） | 11 | 10 | 15 | A4 | A5 |
| B型数量（台） | 10 | 12 | 13 | B4 | B5 |
| C型数量（台） | 15 | 8 | 12 | C4 | C5 |
（2）根据C型空调前三周的销售情况，预估C型空调五周的平均周销售量为10台，当C型空调周销售量的方差最小时，求C4，C5的值；
（注：方差s2=$\frac{1}{n}$[x1-$\overline{x}$）2+（x${\;}_{2}-\overline{x}$）2+…+（xn-$\overline{x}$）2]，其中$\overline{x}$为x1，x2，…，xn的平均数）
（3）为跟踪调查空调的使用情况，根据销售记录，从第二周和第三周售出的空调中分别随机抽取一台，求抽取的两台空调中A型空调台数X的分布列及数学期望．
9．
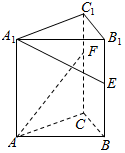如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）
如图，在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1，CC1上的点，且BE=B1E，C1F=$\frac{1}{3}$CC1，则异面直线A1E与AF所成角的余弦值为（ ）| A． | $\frac{\sqrt{3}}{6}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{\sqrt{3}}{10}$ | D． | $\frac{\sqrt{2}}{10}$ |
3．已知命题：p“?x0∈R，x02+2ax0+a≤0”为假命题，则实数a的取值范围是（ ）
| A． | （0，1） | B． | [0，1] | C． | （1，2） | D． | （-∞，0）∪（1，+∞） |